（这个系列原本想写成上、下两篇，上篇写数学，下篇写物理。然而为了科普的完整性，需要介绍20世纪粒子物理的发展史， 由此下篇会变得非常长，无奈只能把下篇继续拆成两篇，而把关于从电子的发现到超弦理论的简介单独成一篇，即为此篇——“中篇”。）
目录
一、引言
二、宇宙的终极原理（柏拉图的第一性原理、长冈模型、狭义相对论和不变量）
三、几何学、群论和不变量 （爱尔朗根纲领、李群、诺特定理）
四、场论、规范场论和标准模型（经典场论、量子场论、强相互作用、弱相互作用、夸克、杨—米尔斯场、规范场论、希格斯机制、标准模型）
五、超越标准模型（标准模型的缺陷、大统一理论、超对称、初代弦论）
六、弦论（粒子物理实验的“分水岭”、格林—施瓦茨定理、第一次超弦革命、卡拉比—丘成桐空间登场）
七、小结
一、引言
1984年。离开丘成桐证明卡拉比猜想已经过去了8个年头，离他正式发表论文也已过去了6年。前一年，丘成桐刚去华沙，接受了颁发给他的菲尔兹奖。这一年，丘成桐为了和妻子生活在一起，从普林斯顿的高等研究所搬到了西海岸的圣地亚哥。
有一天，丘成桐溜达到他妻子的办公室里，忽然接到了来自普林斯顿一台名叫斯特鲁明格（Strominger）的物理学家打来的电话。彼此寒暄后，斯特鲁明格告诉丘成桐，他和他的合作者们正在研究一种叫做“超弦”的（物理终极）理论。这种理论要求世界是10维的，除了相对论隆重推出的四维时空之外，超弦还需要另外的六维空间。这个六维空间要满足物理里的“规范对称”（SU(3)），需要满足爱因斯坦场方程的真空方程，还需要“紧致化”。卡拉比—丘成桐定理所提供的空间的一台特例（实六维、复三维），是符合上述性质的最佳“空选”。
斯特鲁明格打电话向丘成桐确认卡拉比—丘成桐空间（流形）是否满足“超弦”所要求的特性，答案是肯定的。根据丘成桐的回忆，当时他正在他妻子的办公室里，打电话的时候凝视着圣地亚哥拉霍亚的海港，明媚的阳光下，是一望无际蔚蓝色的太平洋，让人浮想联翩。2000多年前，古希腊的泰勒斯面对着家乡米利都海港外一望无际的大海，说出了“万物都来源于水”，开启了人类探求宇宙终极原理的路程。如今，丘成桐面对着大海，也颇为感慨，难道物理终极理论的大门终于要被开启了？
美国加州圣地亚哥的拉霍亚海湾
第二年，包括斯特鲁明格、威腾（Edward Witten）在内的四个物理学家联合写了一篇题为《超弦的真空结构》的论文。这篇论文论证了超弦理论所要求的“多出来的六维”必定藏在卡拉比—丘成桐结构的流形之内。这篇文章是里程碑式的，和“反常消除”、“杂化弦”一起被誉为开启了第一次超弦革命的奠基之作。
1985年，包括威腾在内的四人论文《超弦的真空结构》引入了卡拉比—丘成桐空间（流形），作为超弦理论额外六维的空间结构。
很多年来，物理学家们一直在寻找一种可以统一广义相对论和量子力学的物理“终极理论”（theory of everything，简称ToE），而弦论似乎就是这种理论，一时间使得很多物理学家相当兴奋，也使得数学家丘成桐相当开心。显然，物理学家比丘成桐更加激动，他们要丘成桐确认六维的卡拉比—丘成桐流形是不是唯一的？如果只有唯一一种六维的卡拉比—丘成桐流形，那么ToE貌似就正式确立了。可是，丘成桐（悲伤地？）发现，卡拉比—丘成桐流形的数量即使不是无限多，也是相当庞大的。通俗一点地说，超弦理论没法确定“多出来的六维”的空间结构，这就有点糟糕了。
丘成桐早在1985年就强调卡拉比—丘成桐流形具有很多种，为火速升温的超弦理论泼了点冷水。不过物理学家表示，这不是个事儿，我们可以搞定这个问题。超弦理论或是依旧持续升温，卡拉比—丘成桐的名声也越来越响，但是无法确定卡拉比—丘成桐空间结构这个问题始终挥之不去，超弦理论最终或是冷了下来。要等到90年代中期所谓的“第二次超弦革命”，弦论才再次红火了一阵子。
上面只是一台引言，顺带了一些物理术语。要更好地理解“弦论”以及卡拉比—丘成桐空间的物理意义，我们必须要介绍一下粒子物理学的发展史，这才可以明白物理学家们到底在做什么。
本来只想简单地介绍一下粒子物理学发展史，没想到下文却写了一大篇，篇幅上只能让这份简介单独成一篇，是为这个系列的“中篇”。
好吧，按照“言必称希腊”的古训（何某人的粉丝除外），我或是从柏拉图说起。
二、宇宙的终极原理
2.1 第一性原理溯源
历史上，有一批哲学家认为，宇宙必然有一台不变的“终极原理”，或者说“第一性原理”（first principle）。这个看起来纷乱的宇宙，其实是可以由这个终极原理来解释的。
物理学家受到了这种思路的影响（毒化？），直到今天。大家如果对人类的思想史有兴趣，可以看看我的另外一台正在撰写的系列，《万物本原探索史》：
我们不从最古老的说起，直接跳到古希腊的哲学家柏拉图。柏拉图老师一生留下了不少对话录，其中有一篇名叫《蒂迈欧篇》的对话录里，柏拉图在其中大搞数学建模。
当时的希腊学界认为，自然界是由四种元素构成的：水、土、火、气。柏拉图有个学生证明了凸的正多面体有五种。于是柏拉图就把其中四种正多面体和四种元素对应了起来，认为四元素的“微粒”（原子）恰好就是四种多面体，而构成多面体的三角形可以拆分又组装起来，代表了四种元素之间的转换。至于第五种正多面体（正十二面体则），它的面不是三角形组成的，所以不是世间的元素，而象征着整个宇宙，或者说，是“以太原子”。
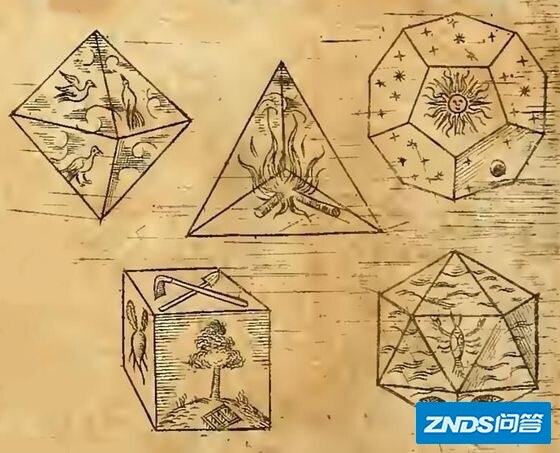
柏拉图模型：四种正多面体分别构成了四种元素的微粒。而正十二面体则是整个宇宙的模型，或者是以太元素的微粒。
柏拉图在2300多年前大搞数学建模，很有意思。更有意思的是，中世纪的时候，西方文明大倒退，柏拉图的对话录就像大部分希腊文献一样，在欧洲遗失了很久，要等到十字军东征以后才重新传回西方。但是这篇《蒂迈欧篇》，却在中世纪前期就奇迹般地保留了下来，对欧洲产生了深远的影响。
虽然四元素的学说和柏拉图的数学建模都早就过时了，但是柏拉图对自然界用数学来描述“第一性原理”这个思路被保留了下来。20世纪初和罗素合作写《数学原理》的数学家怀特海老师说，整个西方文明，就是柏拉图的注脚。
为了避免把这篇文章写成哲学史，就此打住，直接跳到20世纪吧。回顾一下柏拉图，主要是想溯源，为啥大部分物理学家那么热衷于建立一台大一统的终极理论，这是有历史原因的。
当然，不是所有的哲学家都喜欢第一性原理和大统一的终极理论。比如，柏拉图的学生、亚里斯多德就非常不喜欢柏拉图用几何学模拟自然的方式，而是喜欢分类、分类、再分类，用博物学家的方法来分类世界。
有可能柏拉图的思路是错的，谁知道呢。但是追求终极理论，现代物理学家叫做theory of everything （ToE），凝聚了很多代聪明人类孜孜不倦的努力。
下面我们来看看20世纪初，两个试图把物理学图像统一起来的人。
2.2 长冈模型
先说第一台人。他是个日本人，叫做长冈半太郎。
我们知道英国物理学家汤姆逊老师在1897年发现了电子，第一次打开了原子内部的结构。于是老汤在1904年建立起第一台原子结构的模型，被称为布丁模型。老汤认为，带负电荷的电子分布在原子中间，而正电荷则均匀分布在原子中。原子结构如下图所示：
汤姆逊的原子模型，第一台具有亚结构的原子模型
长冈半太郎原本是一台武士的儿子，明治维新后留学欧洲，成为了一台物理学家。他是在物理最前沿领域做出贡献的日本第一代物理学家。长冈发现老汤的布丁模型有破绽：电子无法穿过如此“庞大”的均匀正电荷介质而成为自由电子。于是，长冈类比土星和土星环的模型，在同年（1904年）给出了第二个原子的结构，被称为原子的“土星模型”。
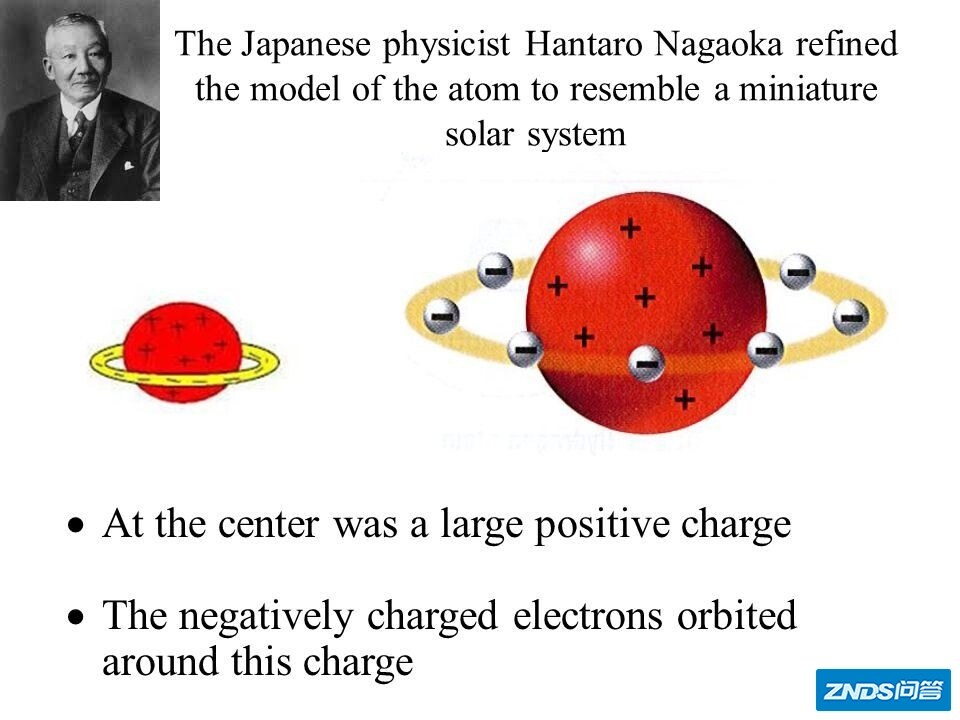
长冈模型，来源：https://slideplayer.com/slide/10719184/
1904年，人们还不知道原子核（要等到1911年卢瑟福散射实验才验证了原子核的存在），所以长冈的模型是相当超前的。当然，长冈并没有明确地表示出“原子核”的概念，他的模型完全来自于宏观（土星和土星环）和微观的类比。
这种试图在宇宙宏观和原子微观建立统一图像的思路，其实是当时的一种终极目标，即认为大自然的结构具有一种“自相似性”，也就是一种跨越了几十个量级的尺度还可以存在的相似结构。
当然，长冈的模型是错误的。很多人认为长冈半太郎没有学好电动力学，其实也是冤枉了他。电磁辐射的理论、特别是特别是带电粒子辐射的势能公式李纳-维谢势（Lienard–Wiechert potential），是由李纳和维谢分别在1898和1900年推导的，而远在日本的长冈可能并不知晓。后来1911年卢瑟福发现了原子核，得到了一台长冈模型的升级版，也就是原子的“太阳系模型”，可惜和长冈模型一样，这样的模型是错误的。和行星环绕太阳不同，圆周或者是椭圆运动的电子会辐射电磁能量，电子的轨道将在极短的时间内螺旋向内，最终塌缩到原子核上。
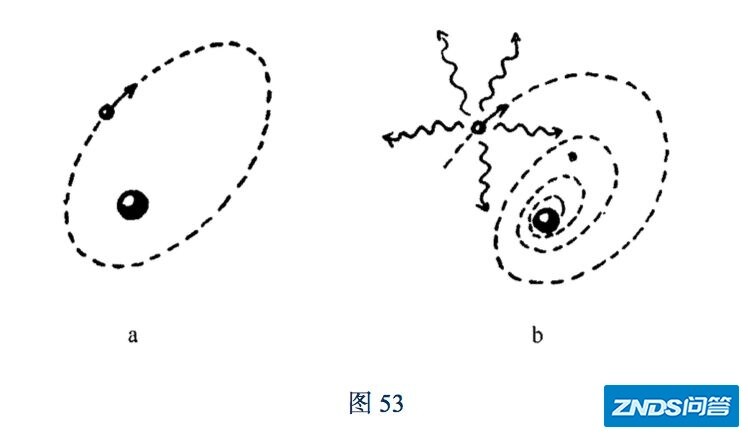
加莫夫著名的科普《从一到无穷大》里给出行星模型（左）和原子的“星系模型”（右）的区别。电子辐射能量，很快塌缩到原子核上。经典电动力学在微观世界必须被“封印”。为啥呢？没人知道。
就在卢瑟福提出“原子太阳系”模型的时候，有一台名叫尼尔斯·玻尔的丹麦年轻人正在卢瑟福门下留学。为了绕开经典电动力学的辐射造成的原子不稳定姓，波尔另起炉灶，强行规定了一套围观世界的发展，用来解释围观电子能级和宏观光谱辐射之间的联系。这就是著名的氢原子“波尔模型”。
如果你是一台那个时代的人，你很大概率会认为波尔的氢原子模型非常糟糕，他几乎是凭空捏造出了一套没有任何根据的微观世界的法则。但是没有办法，经典电动力学没法解释原子内部结构，所以电动力学必须在微观世界被强制“封印”。为了对比观测，物理学家们必须另起炉灶，建立起一台全新的理论，波尔也成为了量子力学的一代宗师。波尔之后，1920年代德布罗意提出了物质波的概念，海森堡、波恩和薛定谔又给了量子力学以数学表达（矩阵力学和波动力学），为量子力学奠定了（形式上的）数学基础。
后来海森堡又提出了“海森堡测不准原理”，波尔提出了量子力学的“哥本哈根诠释”，量子力学正式和经典物理分道扬镳，成为了一种概率计算的理论，这也开启了爱因斯坦和波尔长达N年的争论，最终老爱败北。不过直到今天，如何理解量子力学或是一台争论的话题。
这些都是量子力学里耳熟能详的故事，我不打算在这里重新絮絮叨叨一遍上面的各种细节，那样太偏离卡拉比—老丘的主题了。回过头来看长冈模型，虽然已经过时了超过一台世纪了，到底还有什么意义呢？
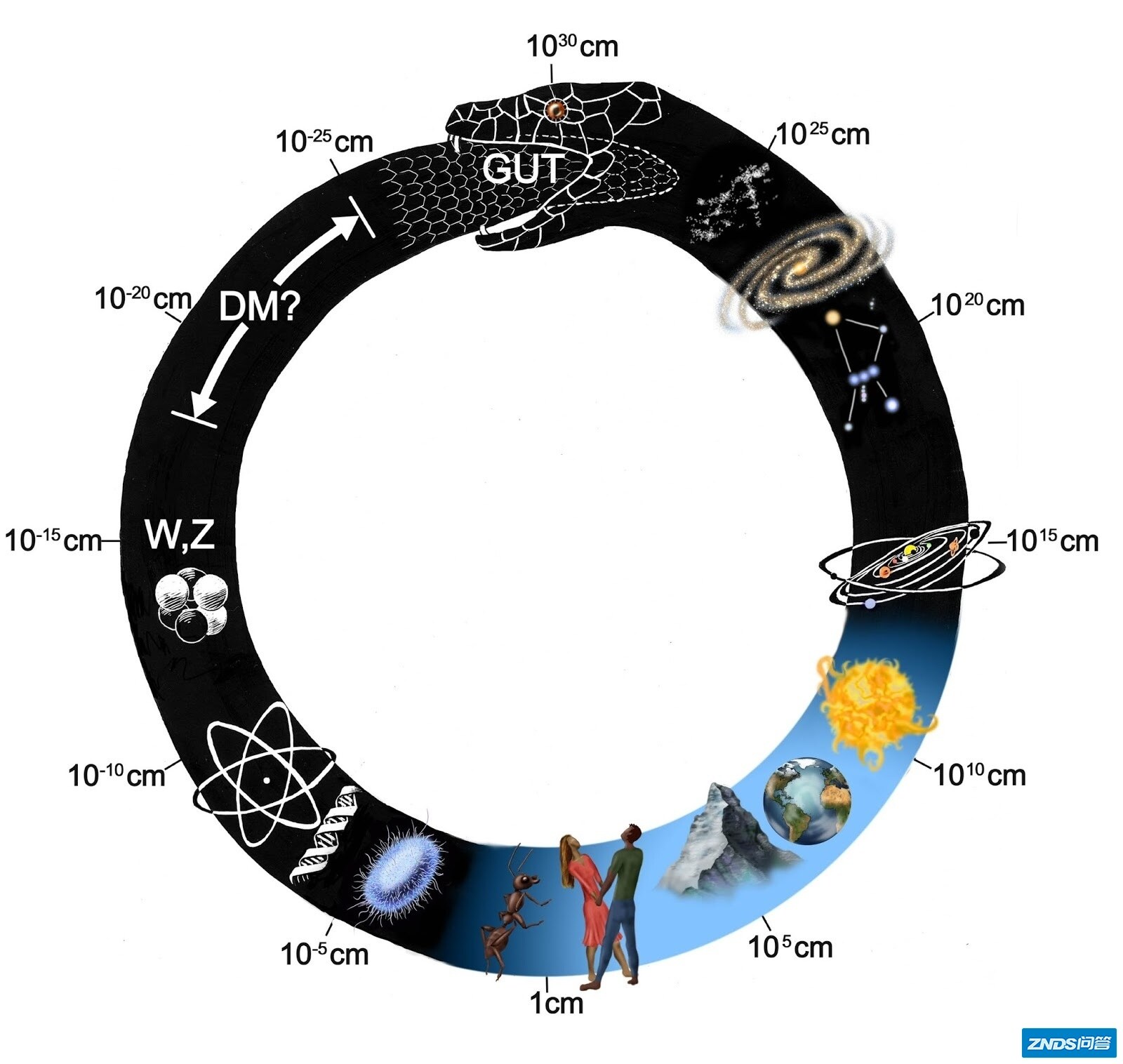
意义就在于，这是统一宏观世界和微观世界的第一次尝试。今天我们经常会看到一张蛇咬着自个尾巴的图，表示最小的微观和最大的宏观联系在一起的，或是很有点长冈的感觉。当然，这条蛇叫做ouroboros，来自古埃及，比长冈古老的多。
量子力学单飞后，由量子力学自个走向统一理论的路子是不行了。我们让量子力学的子弹飞一会，再来看看别的物理领域。
这就要说第二个人了——大家耳熟能详的爱因斯坦。
2.3 狭义相对论和不变量
爱因斯坦为啥要提出狭义相对论呢？
一台最基本的出发点，就是要建立一台经典力学（牛顿力学）和经典电动力学的统一理论。
在爱因斯坦之前，已经有一批学者试图建立两者之间的统一理论了，但是他们的理论都相当糟糕，在电动力学上打上了牛顿力学的补丁，其代表人物，就是荷兰物理学家洛伦兹。
爱因斯坦和洛伦茨（1921年）
20世纪初的物理图像是这样的：光和电磁波作为波的存在，都是通过一种叫做“以太”的物质传播的（注意，前面说过，柏拉图同学在《蒂迈欧篇》里就开始讨论以太了。）但是这个以太非常难搞，完全测不到它的本尊（有点像目前的暗物质）。而且另外的实验显示，光速无论光源的运动如何，似乎都是不变的。
于是物理学家们为了让以太的性质符合实验和观测结果，强行给以太打上了补丁，比如以太阻力很大，会在物体前进的方向上压缩物体。而物体在自个运动的参考系里，会有一台假的“当地时间”。通过这些补丁，物理学家们就可以解释光在以太中的速度不变了。
用数学公式表达，就是运动物体的参考系和以太的“绝对参考系”之间的一台变换公式。比如，洛伦兹在1892年给出的公式如下（original的部分）：
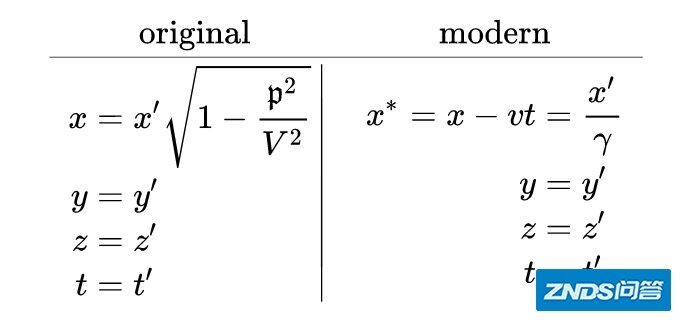
这个公式，和狭义相对论里的洛伦兹变换几乎一模一样（所以叫洛伦兹变换，不叫爱因斯坦变换）。
爱因斯坦的贡献是指什么呢？
爱因斯坦认为，洛伦兹变换，不仅仅是运动物体和以太的“绝对空间”的坐标变换公式，而是任意两个参考系之间的变换公式，这就是“相对论”的字面意义。既然没有坐标是特殊的，那为啥还要留下以太这个“绝对空间”呢。于是爱因斯坦把绝对空间这个概念扔掉了，把以太这个概念也扔掉了。
好了，物理学先说到这里，数学家可以出场了。
庞加莱和爱因斯坦唯一的合影，1911年索尔维会议。另外这里还有居里夫人、卢瑟福。坐标懒得标了，熟悉物理的人肯定找的到。
爱因斯坦是1905年6月30日（发表于九月份）隆重推出他的狭义相对论论文《论动体的电动力学》的。
然而早在6月5日，法国数学家庞加莱也推出了洛伦兹变换，以下是庞加莱的公式：
庞加莱令  ，这就是妥妥的洛伦兹变换。
我们今天说，庞加莱老师和洛伦兹老师一样，虽然推出了洛伦兹变换，但是把这个变换公式看成是运动物体建立的坐标和以太空间之间的变换，而不是任意两个（没有引力的）参考系之间的变换。所以，狭义相对论的创立者，还得归功给爱因斯坦。
至于庞加莱到底是如何想的，这个就留给考据学家去考察，这里不再讨论。不过我想说的是，老庞毕竟是老庞，就是比别人高屋建瓴。在那年的七月份，庞加莱又写了一篇文章，在那篇文章中，庞加莱提出了著名的表述：
洛伦兹变换，其实就是四维时空里的一台坐标旋转。
为了解释什么是四维时空的坐标旋转，我们先来看一台基本的例子，即平面直角坐标的旋转：
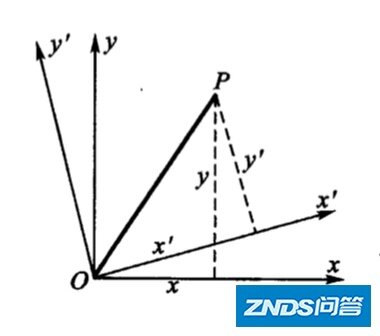
坐标旋转变换
对于坐标旋转一台角度  ，则坐标变换为：
把二维的情况推广，我们可以建立起一台矩阵的乘法来表示坐标变换:
如果坐标变换后的向量长度相等，也就是  ，我们定义这样的变换为“正交变换”，俗称即是“坐标旋转”。
狭义相对论的洛伦兹变换，本质上对应于一台伪四维欧几里得空间的坐标变换：
这里引入了一台伪四维欧几里得坐标，因为其中第四维  带有一台虚数，所以被称为“伪”，或者“赝”。那么上面这个坐标变换，使得向量长度  距离不变的变换，也就是说，这个变换是伪欧式空间的一台正交变换。洛伦兹变换对应的矩阵，也就是伪欧氏空间里的一台正交矩阵，几何上等同于一台坐标旋转。
但是，上面的坐标变换只是千万种洛伦兹变换里的一种，也就是对应于三维参考系在x方向有运动的特例。线性代数告诉我们如何从一台“正交矩阵”推导出另外的正交矩阵。各种各样的正交矩阵，也就是各种各样的洛伦兹变换，组成了一台集合，也就是一台群。
用更数学化的语言来表述洛伦兹变换：
- 所有的洛伦兹变换组成一台群，即洛伦兹群。洛伦兹群是伪四维欧几里得空间（闵可夫斯基时空中）的一系列的“坐标旋转”。
- 电动力学里的麦克斯韦方程组，还有狭义相对论里的运动学，在洛伦兹群下保持协变性。
- 所有使得伪四维欧式空间
 距离不变的坐标变换组成的群，被称为“庞加莱群”。“洛伦兹群”是“庞加莱群”的一台子群。
- 相比之下，牛顿力学只在伽利略群下保持协变性，而在洛伦茨群下则协变性遭到了破坏。
庞加莱把洛伦兹变换和狭义相对论建立在群论和不变量的基础上。
由此，群论在物理学里登场了。从此，群论成为了物理学里一台很重要的数学工具，并逐渐成为物理学的主流。
那么，庞加莱为啥要把当时物理学家尚不熟悉的群论引入狭义相对论呢？那是因为庞加莱想用群论和不变量来“统一”物理学的语言。
因为在庞加莱之前，德国数学家克莱因已经用群论统一了当时的大部分几何学，群论和不变量的观念已经在数学界深入人心了。
让我们回到19世纪的数学界去围观一下。
三、几何学、群论和不变量
3.1 爱尔朗根纲领
19世纪，几何学进入战国时代，其中几个比较重要的几何学分支为：
- 欧几里得几何学的高维推广。欧几里得几何学在很长时间限定在二维（平面几何）和三维（立体几何），后来由于解析几何和高次代数学的发展，促生了高维的欧几里得几何学。
- 射影几何。文艺复兴时代的美术透视法是射影几何之滥觞，而为射影几何奠定坚实数学基础的，是19世纪初的法国数学家彭赛列（Poncelet）。老彭跟随拿破仑东征俄国，战败被俘，在战俘营里什么书都没有，于是一台人怒刷射影几何。
- 仿射几何。这门几何学很像欧氏几何，但是没有角度和距离的概念。仿射affine这个词，最早是由18世纪的欧拉发明的，后来被19世纪的莫比乌斯详细讨论（就是莫比乌斯带的那个老莫）。
- 非欧几何。非欧几何学的故事说来话长。简要来说，非欧几何原本是围绕“平行线公设”的讨论展开的，按照公理化体系讨论的，被称为罗巴切夫斯基几何。按照微分几何方式讨论的，被称为黎曼几何。
- 度量几何。后来人们发现，非欧几何其实可以在曲面上实现。其实球面几何就是一种最早的非欧几何，而镶嵌在四维欧氏空间中的三维曲面可以用来模拟非欧几何。贝尔特拉米（Beltrami）首先认识到曲面和非欧几何空间的关系。由此，罗氏几何也被称为“双曲几何”，而黎曼的几何被称为“椭圆几何”。
面对着种类繁多的几何学，有人开始尝试用“更高的观点”把几何学统一起来。
1872年，23岁的德国数学家克莱因（Klein）在爱尔朗根大学发表了一篇划时代的报告，叫做《新几何研究上比较的观点》，俗称为《爱尔朗根纲领》。在文中克莱因把群论引入了几何学，并用群论统一了上述的各种几何学。
德国数学家费利克斯·克莱因（1849－1925）
群论是由19世纪初的法国天才少年伽罗华为了讨论多项式方程的根而发明的理论。伽罗华的群论长期遭到数学界的冷落，随后被运用在代数学里。群论第一次被引入几何学的，正是克莱因的《爱尔朗根纲领》，这就是为啥说这篇报告有着划时代的意义。
按照克莱因的观点，每一种几何学，对应一种群（被称为变换群）。而几何学的目的，就是为了研究在其对应的变换群的变换下的“不变量”。
克莱因把当时所有的几何学，都归为射影几何学。而射影几何学的目的，就是研究从一台空间到另外一台空间上的变换群下的不变量。比如，三维齐次的变换形式可以表达成：
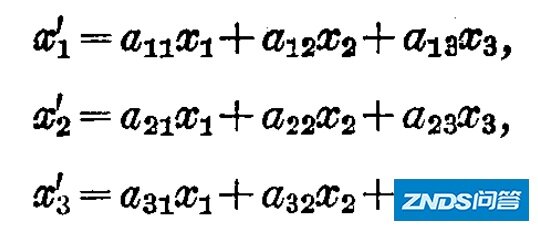
射影几何在群变换后研究的不变量包括了：线性（直线被变换后或是直线）、相交性（相交线被变换后或是相交线）、交比、保持圆锥曲线不变等等。而满足上述性质的变换群，即被称为“射影群”。
射影群的一台子群，被称为“仿射群”，对应于仿射几何的变换。仿射几何具有和欧氏几何相当类似的不变量，但是角度和长度是会改变的。
欧氏几何对应的变换群又是仿射群的一台子群，其不变量是旋转、平移和反射。
以下是一台示意图，表示了从射影几何—> 仿射几何 —> 欧氏几何的层层递进。其中列举的不变量，欧氏几何不变量：角度、距离和面积。仿射（affine）几何不变量：平行。射影几何的不变量：相交。
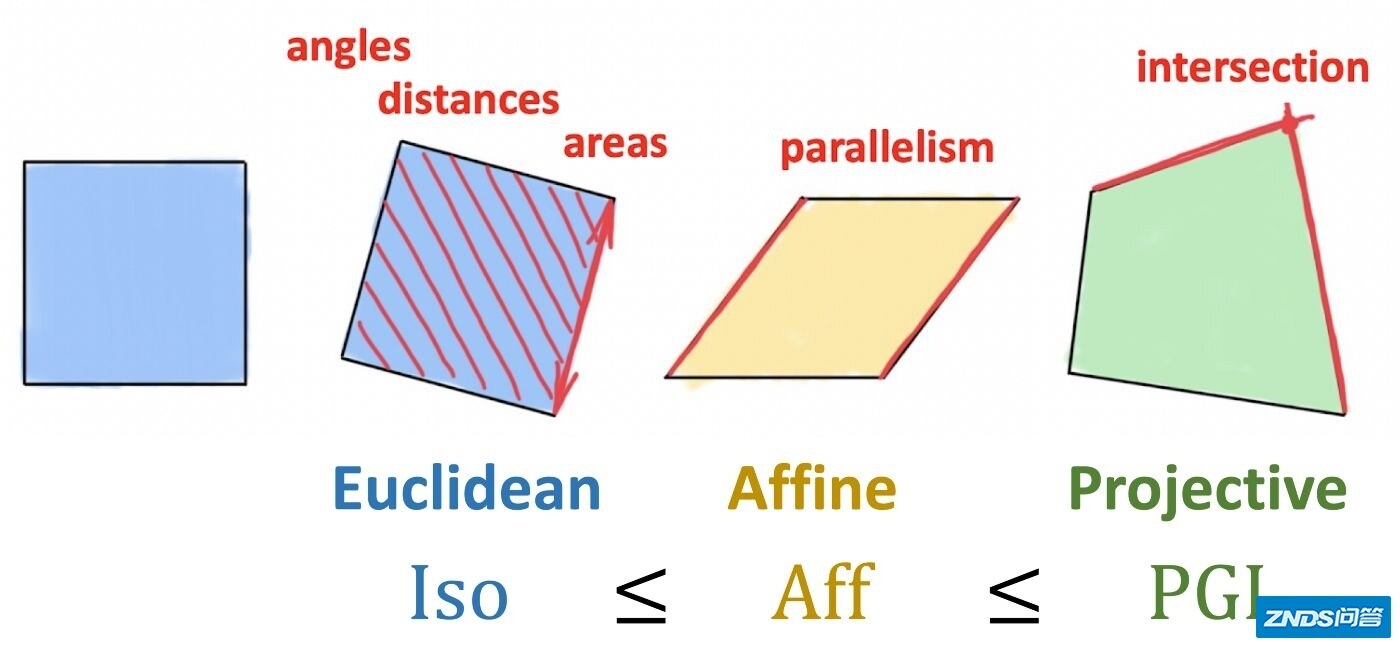
来源：https://towardsdatascience.com/geometric-foundations-of-deep-learning-94cdd45b451d
另外一台更完整的《爱尔朗根纲领》在群论下统一当时的几何学各分支的示意图如下：
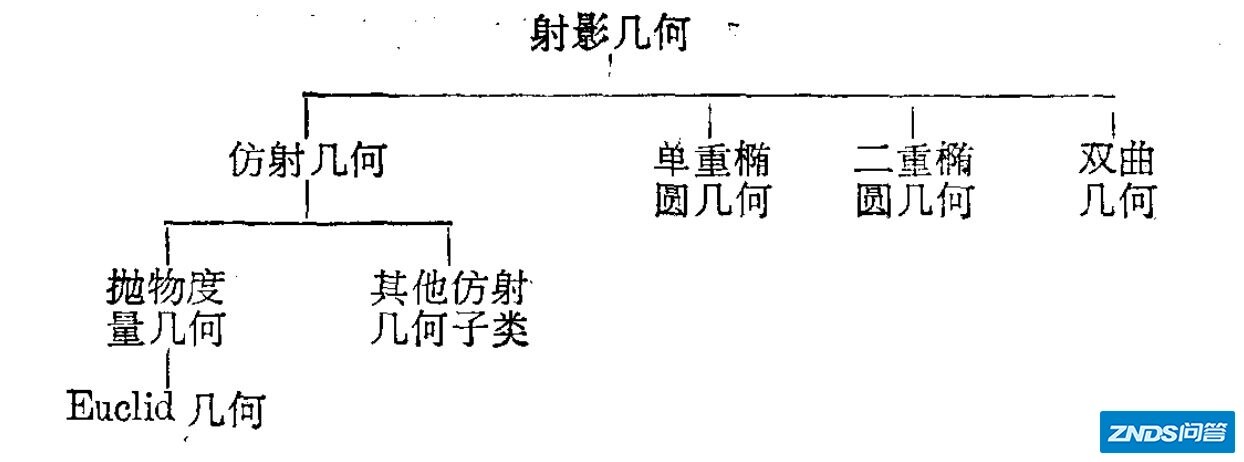
来自克莱因《古今数学思想》第三册
值得一提的是，《爱尔兰根纲领》只有20多页，其中没有一台数学公式，但是却具有极重要的意义。数学论文不一定需要有数学公式！
《爱尔朗根纲领》里所强调的变换群，在今天看来，是一种更广泛的群——李群的被称为“经典群”的特例。克莱因发表《纲领》十几年后，1884年，克莱因的好朋友、挪威数学家索菲斯·李在克莱因的基础上更详细讨论了变换群，他的三卷本的《变换群理论》引入了一般的连续变换群，今天的人称之为“李群”。
挪威数学家索菲斯·李（1842-1899），系统研究了“李群”。李老师是克莱因的好基友，没有克莱因强调群论的重要性，也不会有李老师对克莱因变换群的推广工作。
李群原本是数学家的游戏，威廉·基灵和嘉当继续发展了李群（还有李代数）。20世纪初，李群被大数学家外尔介绍进入了物理学，很快成为了物理学不可缺少的基本工具，我在后面很快就会谈到。
另外，《爱尔朗根纲领》里只考虑了均匀的空间，所以当时正在兴起的黎曼几何并没有被克莱因的变换群论囊括其中。但是不久之后，数学家们就把黎曼几何的“局部不变量”和克莱因的思想（变换群）结合起来。其中一台很有名的结果，叫做“嘉当联络”，不过就不在这里就不做过多解释了。
最后再说说庞加莱为啥会在第一时间就把洛伦兹变换和群联系起来，发现洛伦兹变换的本质对应于伪四维欧氏空间的一台保持等距的群？这是因为庞加莱对《爱尔朗根纲领》再熟悉不过了，他自个也对群论做出了卓越的贡献。在庞加莱眼里，狭义相对论和群论之间具有联系，是再明显不过的了。
3.2 诺特定理：不变性、对称性和守恒律
下面我们再回头来看物理。
我们知道，牛顿力学有两个“花式”升级版，一台叫做拉格朗日力学，一台叫做哈密顿力学。下面我们来回顾一下拉格朗日力学：
一台系统内的动能为T，势能为V，则可以给出拉格朗日量（简称拉氏量）  ，而拉氏量可以写成时间  ，广义坐标  和广义动量  的函数 ：
则拉氏量满足欧拉—拉格朗日方程：
 ,
其中  为系统对应于 i 分量上的非保守力。对于完整的系统则  。
欧拉—拉格朗日方程原本是18世纪所谓“分析的世纪”中数学家把牛顿的物理定律从几何学的图像转化为偏微分方程的一种数学表达形式，本质上和牛顿运动定律完全等价，但是从牛顿的几何学方式过度到求解微分方程的分析方式，更适合推广。
到了20世纪初，德国数学家艾米·诺特对拉格朗日方程有了新的解读。诺特把群变换、不变量和物理的守恒定律联系了起来。
前面提到1872年克莱因在德国的爱尔朗根提出了著名的《爱尔朗根纲领》用来统一几何学。整整十年后，艾米·诺特在同一所城市出生了。诺特的父亲就是一位数学家，在爱尔朗根大学当数学教授的时候生下了艾米·诺特。当时的世界对于女人研究数学是很不欢迎的，但是诺特或是顶住了压力，做出了卓越的数学成就。1915年，已经在哥丁根大学数学系势如中天的克莱因和数学泰斗希尔伯特联合邀请诺特去哥丁根大学，但是诺特依旧得不到一台正规讲师的编制。
德国女数学家艾米·诺特（1882－1935），一生坎坷。
刚到哥丁根大学，诺特就发现了在拉格朗日力学框架下，物理守恒量和无穷小变换下不变量之间的对应关系，被称为“诺特第一定理”，简称诺特定理。
具体地来说，在经典力学的框架下，如果时间在  的无穷小变换下，作用量
的变分依旧为零 （通俗地理解，可以看成拉氏量不变），那可以证明
不变。而  恰好就是系统的总能量，代表了能量守恒。
如果空间的广义坐标在  的变换下，作用量不变 , 那就有：
是个不变量，对应了系统在第i个分量上的动量守恒。
诺特定理把时间和空间平移下拉格朗日作用量的不变性和物理守恒定律联系了起来，最常见的三个联系就是：
- 时间平移的不变性 --> 能量守恒
- 空间平移的不变性 --> 动量守恒
- 角度旋转的不变性 --> 角动量守恒
从数学上来说，对时间、空间和角度做无穷小的变换，对应于一维的李群变换。用《爱尔朗根纲领》的语言，一维李群作用下的不变量，必然对应一种几何学，而这种几何学在物理上则恰好对应于各种守恒定律。
这种把几何学和物理联系起来的观点，最早来自于19世纪的德国数学家黎曼和物理学家赫兹，而被狭义和广义相对论发扬光大。诺特定理的诞生时间，正是哥丁根的希尔伯特正在和爱因斯坦竞争（合作？）推导广义相对论场方程的1915年，而背景则是哥丁根正在讨论关于广义相对论里的“能量”是否依旧守恒。
上面给出的诺特定理是在经典力学的框架下描述的。相当重要的是，诺特定理可以推广到狭义相对论和量子力学。
值得一提的是，在物理里，更多人喜欢使用“对称性”这个词。
对称性，说的是物理系统的一台状态通过一台变换群变成了另外一台状态，而这两个状态等价，这说这个物理系统在该群变换下是“对称”的。所谓的“状态等价”，则是用不变量或者协变性来描述的。比如，在一维李群无穷小变换下的拉格朗日作用量不变（不变性），则说该系统对于李群无穷小变换是对称的。又比如，麦克斯韦方程在洛伦兹群下是变化的，但是这种变换满足协变性，则说麦克斯韦在洛伦兹群下是对称的。
所以，诺特定理，按照对称性的语言再说一遍，就是每一种对称性对应于一台守恒定律。
我们后面可以看到量子场论里，拉格朗日量不再是动能减去势能这么简单了，而是变成了这种样子（后面会仔细说）：
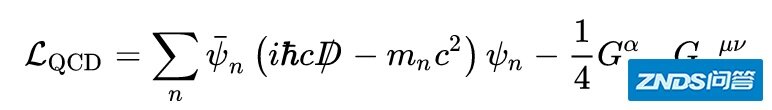
拉氏量在量子场论里几乎起到了“中流砥柱”的作用（或许就是来自于诺特定理的影响力）。基于拉格朗日量对称性和守恒量之间关系的诺特定理，也成为了量子场论里相当重要的定理，这是诺特所不曾想到的。
已经说到了量子场论，下面我们就来看看场论，从经典场论说起。
四、场论，规范场论和标准模型
为了介绍如何把对称性引入场论，我们首先要介绍，什么是场论。
4.1 为啥要研究场论
牛顿力学的内核就是牛顿三定律+万有引力定律。
一开始，人们并不重视场论。虽然牛顿时代的哲学家们批评牛顿版的万有引力具有神秘的“超距作用”（即物体不接触就能产生作用），但是这些争论仅仅是哲学层面上的。数学家认为，把一台系统里每个物体受到的力写下来，认认真真地把方程解出来，就可以模拟（预测）系统未来的状态。
这是一种典型的机械宇宙观：对一台系统给定初始值（受力情况、初始速度），就可以把这个系统的未来算出来。目前还有很多人认为牛顿力学就代表了机械宇宙观。
但是，尴尬的事情发生了。刘慈欣很清楚这个尴尬，那就是三体问题。具体的说，三个相互之间具有万有引力的物体，在数学上是没有解析解的。
下面就是三体问题的普遍方程：
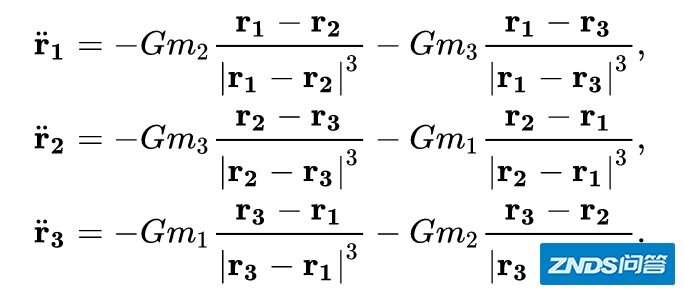
三体问题的普遍方程。
二体问题早就被牛顿解决了。但是虽然数学家们很努力地求解上面三体问题的方程组，却总是找不到解析解（普遍的非数值解）。后来数学家们才恍然大悟，解不出来的最关键原因，是因为方程的个数要大于限制条件的个数（更专业一点的说法：一阶微分方程的个数大于代数积分的个数），所以我们不可能得到三体问题的解析解。
如果要强制搞数值解，三体问题也会遇到了混沌效应，可以感受一下三体问题的数值解：
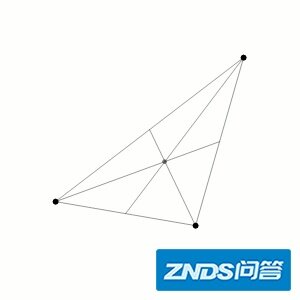
就连三体问题都没法好好求解，更别提真正的大自然了。这当然让数学家们脸上无光，于是数学家们另辟蹊径，发明了一种求解系统内物体（质点）运动的方法：既然不能把一台系统内所有物体的运动给解出来（全局解），那么我们就先每次只关注一台物体（局部解）。这个物体除了满足惯性定律之外，还被所有别的物体产生的叠加力所作用，这个叠加起来的力在满足一定的条件下即被称为“场”。
也就是说，按照18世纪的观点：场，就是把多体问题中的一台物体A孤立出来，把别的物体对A的作用，转化为一台空间的背景，也就是“场”，从而追踪A在作为背景的场中的运动。
严格地来说，物体A在场中运动，A的“自生场”会改变“背景场”，情况会变得很复杂。为了更简化问题，很多时候我们不考虑A对背景场的影响，而把A说成“测试质点”。
可以回顾一下地面上物体自有落体的情况，这是最简单的场论：
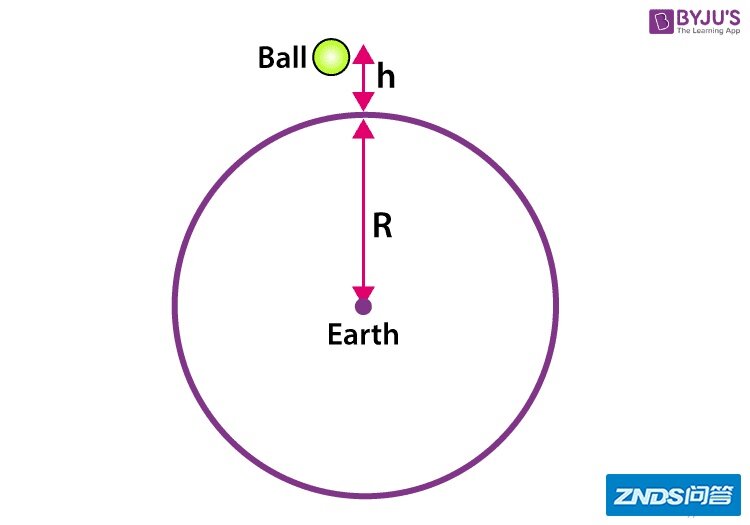
与其考虑地球和小球的“二体运动”，我们不如说小球处在地球的“引力场”中。更关键的一点是，小球本身是个“测试质点”，小球本身的引力场对地球的场不产生影响。虽然这不是严格的数学理论，但是一系列的近似处理都是合情合理的。
对于更复杂的情况，数学家们可以把场的方程写出来。比如最著名的就是拉普拉斯方程和泊松方程，对于平方成反比的力产生的（稳态）标量场：
上面是泊松方程，如果右边为零，则是拉普拉斯方程。
当然，拉普拉斯和泊松的时代，还没有场（field）这个词，而数学家们更喜欢用“势能”这个词。虽然引力场被18世纪的数学家们讨论了很久，但是“场”（field）这个词正式被使用的第一人，却是几乎不懂数学的法拉第，用来形容电场和磁场的。下面是法拉第在1852年画的可视化的磁场分布图：
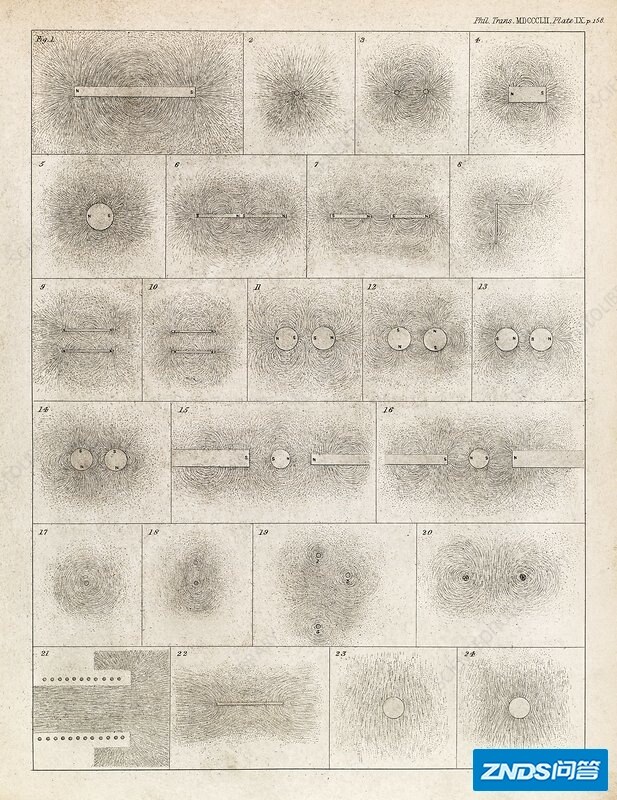
法拉第描绘磁场分布（1852年）
比较有趣的一点就是，在电磁学里，电磁场不再依赖于物体，而可以单独存在。
举个例子。
前面说到拉格朗日量  ，也就是动能减去势能。牛顿可能会不服气：这是指什么嘛，不就是把我的理论给花式数学化嘛，没什么本质的变换。
但是，在电动力学的框架下，没有物体的真空中也可以有拉氏量：
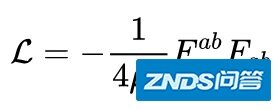
从拉氏量出发，则可以得到真空的电磁场方程。
一会儿我再来介绍上面方程的符号  。先来敲一下黑板：上面的拉氏量完全超越了牛顿力学，这是当初费劲力气解三体方程的欧拉、拉格朗日和泊松从未想到过的问题。
但是，话说回来，即便是在电磁学和电动力学的框架里，多体问题依旧没有解决。编写《经典电动力学》的Jackson说过，电动力学只能解决已知电磁场下粒子的运动，或者已知粒子运动而求电磁场，却无法把两者结合起来。经典电动力学框架下的粒子运动方程式，至今或是一台未解难题，这里就不仔细展开了。
说到这里，经典场论说得差不多了，下面我们来看看量子场论。
4.2 量子场论
量子场论是个很大的话题，我们来看看，能不可以用比较直观的方式来抓住量子场论的本质。
量子场论的本质，是用“量子场”的方式处理多个粒子生成、消灭和相互作用的问题。所谓的“量子场”，说的是每一种基本粒子都对应一台场。
对于单个电子（比如氢原子中的电子），我们有薛定谔（Schrodinger）波动方程来描述非相对论性的电子，又有狄拉克（Dirac）方程描述（狭义）相对论性的电子。但是如果有两个和以上的电子，薛定谔方程和狄拉克方程就不能给出它们的精确解了。朝着这个方向发展的多体理论，进入了“量子纠缠”、“量子计算”和“非相对论型量子场论”的领域，我们不去说它。
量子场论的出发点，是来自于狄拉克方程。这在于从薛定谔方程（非相对论性）--> 狄拉克方程（相对论性）电子方程的推广过程中，出现了让人难以理解的“负能量问题”。狄拉克发现，他的单电子相对论方程（狄拉克方程）存在负能量的解。我们知道，根据狭义相对论的公式，能量和动量的关系为：
求能量我们自动选取  ，因为我们已经假定总能量是正的。狄拉克认为，在狄拉克方程中负能量的解  不应该随便被舍弃（这点很好很数学）。也就是说，电子是有可能处在负能级上的。
那么为啥自然界中的电子大都处于正的能级，而不跌落到负能级呢？狄拉克在1930给出了一台被称为“狄拉克电子海”的解释。狄拉克认为所有的负能级态已经都被电子占满，通俗一点地说，负能级已经没有“坑位”了。另一方面，如果一台负能级的电子得到激发，则会让出一台“坑位”，也就是一台“空穴”。这个空穴从观测来看，则是一台具有正能量的，电荷相反的，质量相同的“正电子”。
1932年，正电子被实验证实。
狄拉克开启了量子场论的研究。不过他对量子场论之后的发展很不满意，其中最大的不满意是场论的计算里会出现无穷大，但是物理学家涉嫌使用“作弊的方法”去掉了无穷大。
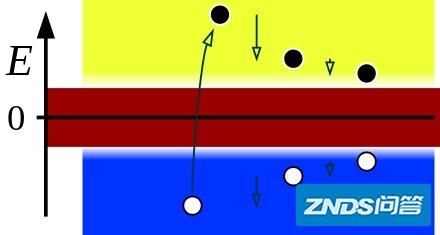
狄拉克的电子海，第一次给真空赋予了负能量的电子状态。电子海最终演化到了量子电动力学：电子是一种量子场存在。
值得一提的是，当时在加州理工的中国物理学家赵忠尧在狄拉克提出正电子不久后就在实验中发现了正电子产生的效应，可惜他当时没有读过狄拉克的理论，所以没有正式喊出“我发现了正电子”的话，于是和诺贝尔奖失之交臂。2年后，老赵的同学安德森“正式”发现正电子，由此荣获了诺贝尔奖，其中的争议，我就不去评判了。
赵忠尧（1902-1998）首次在实验中观测到正电子产生的效应。但是赵忠尧没有听说过狄拉克的理论，所以和“正式”发现正电子失之交臂。
狄拉克的“电子海”是为了解释狄拉克方程的，不过有点让人感到蹊跷：首先，狄拉克方程原本是为了描述一台电子而推出的方程，而最后则描述了“几乎所有”的电子和正电子。第二，具有无限多负能量态的无穷多电子必然具有无限大的能量密度，但是这居然是不可测的，而只有其密度的变化才可以测，这让人费解。另外狄拉克的电子海的图像只适用于费米子，而不适用于玻色子。
很快地，狄拉克电子有了升级版：电子并不是一台单独的粒子，而是来自于一种叫做“电子场”的量子场。狄拉克认为的电子处在“最低能级”，其实是电子场处在最低态（真空态）。电子场的能量是量子化的，每一次激发场，则会产生一台激发态的粒子——电子或者正电子。这样的升级版，开创了一门学问，叫做“量子电动力学”。
我们知道，在量子力学里，描述一台电子的运动，我们可以用电子的“概率波”函数来描述。电子所在的位置只是一种概率的存在，直观地表示如下：
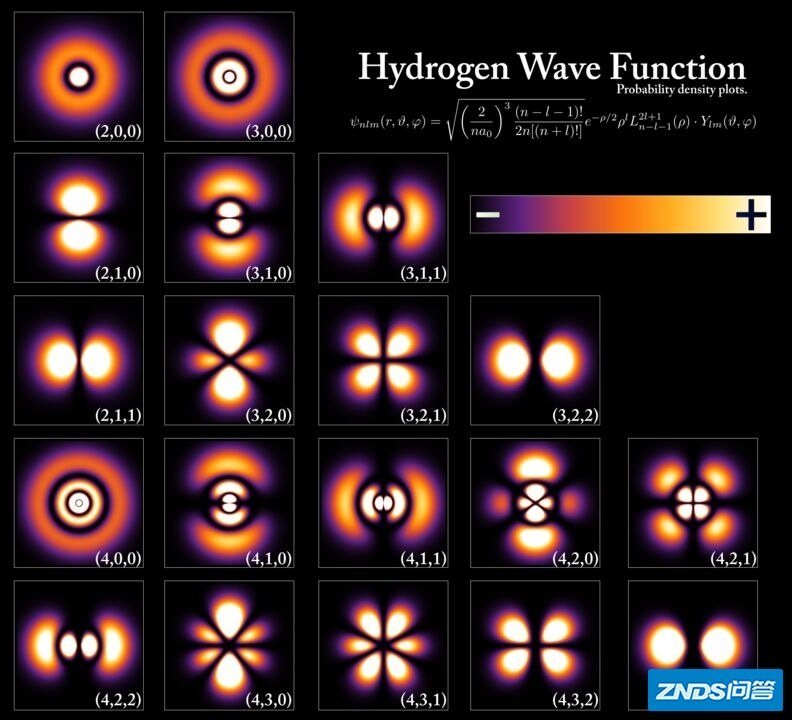
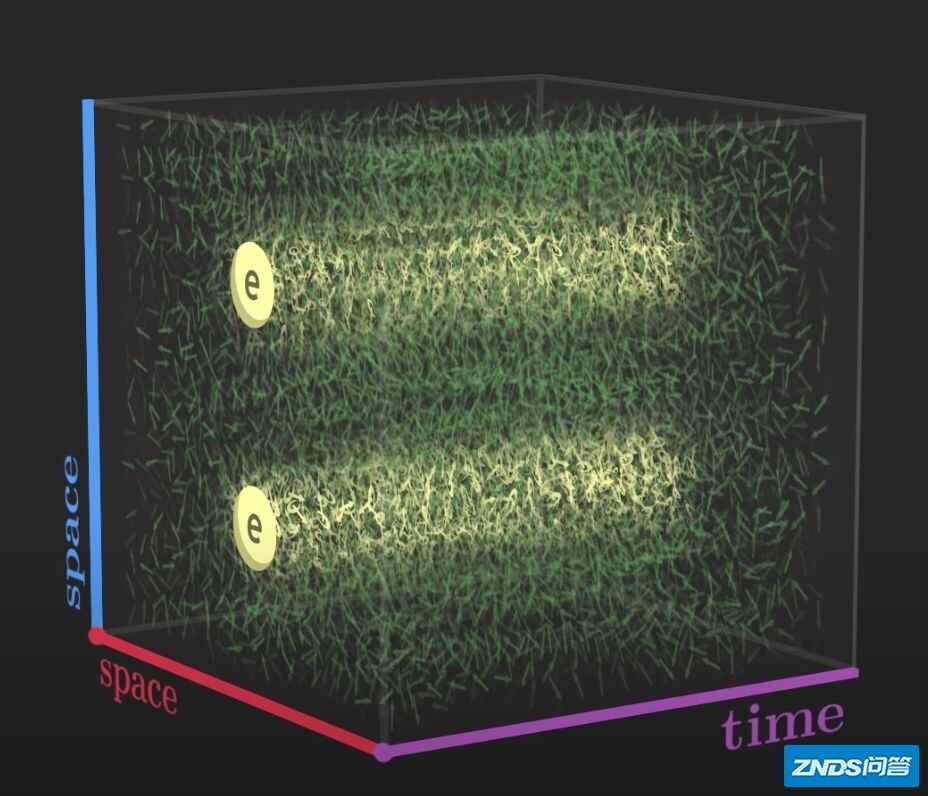
在量子场论中，电子不再被看成波函数的存在，而被看做是“电子场”的真空态的激发。电子场的真空态不断随机生成消灭各种虚粒子，其直观的图像如下：
所以说，量子场的真空充满了“量子泡沫”。电子在这样的量子泡沫里的直观形象是（注意空间被化简成为两维，另外一维是时间轴）：
当然，各种场之间是可以相互作用的。比如，“电子场”和“光子场”的相互作用，可以用拉格朗日量来表示：
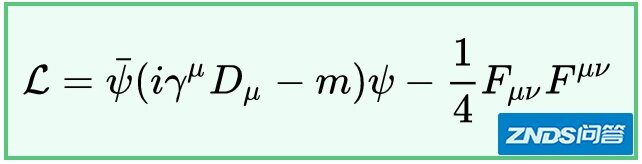
我不打算对上面的方程展开细节性的描述，只说方程中的第一项刻画了电子场（严格地说，是自旋为1/2的费米场）的性质，第二项刻画了光子场（也就是电磁场）的性质。眼尖的同学可以发现，第二项和前面经典电磁场论里的拉氏量，几乎一模一样。
没错，在诺特定理那一节已经说过，拉格朗日量完美地从远古（经典）走向未来（各种现代物理理论），成为了链接经典物理和量子场论的“带头大哥”。
量子电动力学，就是为了认真处理光子和各种粒子的相互作用而诞生的。
量子电动力学自从1930年代狄拉克初创以来，一路和“无穷大”的问题磕磕碰碰，终于在上世纪的40年代末50年代初，通过一种数学家完全不知所云的方式，用无穷大减去无穷大等于有限的方法，自洽地解决了问题（学名叫做：重整化）。
量子电动力学的数学作弊高手，用重整化解决无穷大问题：朝永振一郎、施温格、费曼。没办法，想学物理就得跟着他们的思路走，因为你自个也找不到别的方法处理无穷大问题。
4.3 强相互作用、弱相互作用和夸克
量子电动力学讨论的是电磁作用，其思路自然而然地被推广到了别的相互作用。
很可惜，量子电动力学的方法不能直接运用在强相互作用和弱相互作用上。物理学家又“卡壳”了。
这就要回过头来简单说一下什么是强相互作用和弱相互作用。
弱相互作用，或者说弱力，导致了原子核放射性衰变，比如 衰变。
beta衰变
早在19世纪末期，物理学家就发现了 衰变，也就是放射性原子核放射电子（ 粒子）的过程。在很长的一段时间内，物理学家认为 衰变中能量和动量是不守恒的。奥地利物理学家沃尔夫冈·泡利基于对能量和动量守恒的信仰，在1930年提出，在 衰变中产生出一种叫做“中子”的粒子。
后来1932年中子被发现，之前的假说粒子“中子”被改名成为“中微子”。意大利物理学家费米基于中微子的假说提出了完整的beta衰变的理论模型。后来1950年代第一种中微子被正式观测到，再次成就了一段理论先行实验跟上的佳话。
提出中微子假说的泡利（1900-1958）
再来说强相互作用。
物理学家如果把目光从原子核外的电子转移到原子核，一台自然而然的问题是，带着正电荷的质子之间应该同性相斥，为啥可以挤在原子核这么狭小的空间之内？
后来物理学家们认识到，阻止质子们相互弹开而保持聚集的作用力，是一种叫做“强相互作用”的力。1934年，日本物理学家汤川秀树首先提出了“介子”的假说。类比电磁作用中两个粒子之间相互交换光子，那么质子和质子、质子和中子的强相互作用，是否也在交换着一种粒子？汤川秀树说yes，他提出了强相互作用中交换粒子的假说，并将其命名为“介子”。
汤川秀树（右）和海森堡（1958年在日内瓦）
介子后来被实验室发现了，一开始物理学家很兴奋，后来发现不得了，介子实在是太多了。如果说粒子之间完成电磁作用只需要交换光子，但是强相互作用里的介子，却多的不得了。
人们开始寻找介子们的关系。下面是一台比较有趣的图：
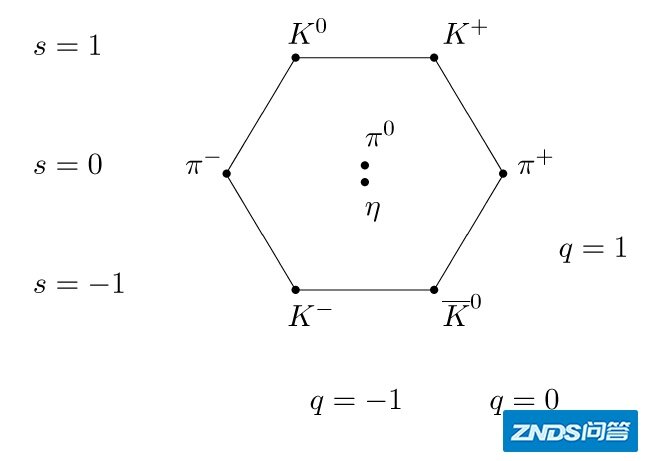
在这张图中一共有八个介子（六边形上一台角上一台，中心两个），随着电荷和自旋属性的不同，可以化成一台六角形的结构。这样描绘八个介子的图示，被物理学家盖尔曼称为“八重态”（其实学名应该是佛教里的“八正道”，物理学家故意翻译成“八重态”以躲避佛教术语）。
八正道
八正道的模型是走向夸克模型的重要环节。
1964年，盖尔曼和茨威格独立地把“八正道”模型升级成夸克的模型，用三种“味”（上、下、奇）的夸克来解释当时多达几百种各种各样奇怪的新粒子。很快夸克模型被扩充成四种“味”（上、下、奇、粲）。到了1974年顶、底夸克也被提出，夸克变成了“六味地黄丸”。
夸克模型的提出者：盖尔曼（左）和茨威格（右）
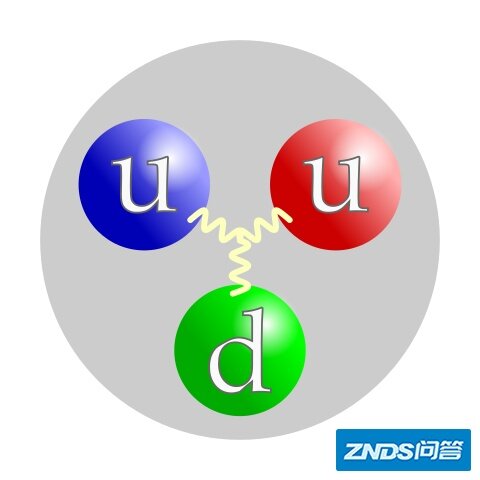
质子由三个夸克组成
那么问题来了。
量子电动力学成功地用量子场论解释了电磁（光）和物质之间的相互作用。那么我们是否可以推广量子电动力学，从而在场论的框架下解释弱相互作用和强相互作用呢？
很可惜，量子电动力学的方法并不能直接运用在弱、强相互作用上。对于弱相互作用，无穷大的问题再次出现了。对于强相互作用，量子电动力学的方法根本是无效的。
物理学家必须另辟蹊径，采用一种新的方法。
为此，要引入“规范场”的概念。
4.4 什么是规范，杨—米尔斯场
规范场论，说的是在特定的李群的变换下保持“量子场”的拉格朗日量不变的理论。
当物理学家们面对着各种各样新发现的粒子，面对着量子电动力学无法被推广到强相互作用和弱相互作的情况，表示束手无措。于是物理学家开始构造各种奇怪的守恒律，还有各种很简单的“对称性”（大家可以回头看一下核物理课本里的那些内容）。
在这种情况下，来自克莱因—李—诺特从群论出发讨论对称性的传统数学，再次统一了粒子物理学。
规范场论的基石，是杨振宁—米尔斯场。
杨振宁（右）和米尔斯
没有杨—米尔斯的理论，就不可能有后来电磁、弱、强统一的标准模型。
规范，原本是来自经典电动力学的“数学游戏”。
在麦克斯韦同学统合电磁学之前，英国的开尔文勋爵曾经在电场和磁场隆重推出一种叫做“矢量场”的东西。我们知道，电场E和磁场B才是可以被观测的量。但是为了给开尔文勋爵一点面子，电动力学中，又定义了一台标量场  和矢量场 ，和电磁场的对应关系为：
我们发现，从一组标量+矢量 可以得到一组电磁场 , 但是反之则不然。只要满足以下的变换：
那么  和 对应于同一组电磁场 。上面的变换，就被称为电磁场的“规范变换”。
为了固定 和 之间的一一对应性，我们必须人为地给定 另外的限制。这个限制不是自然界赋予的，而是人为的，被称为“规范”。对于电动力学，最常用的是“洛伦兹规范”，还有“库伦规范”。
经典电动力学里的规范或是一种“数学游戏”，因为 并不是观测量。但是在量子力学里，1959年阿哈罗诺夫－玻姆效应发现了在量子的层面上 是有观测效应的，由此场的规范效应是有实际物理意义的。
回头来看电磁场在量子力学情况下的“规范”。大数学家外尔首先证明了，量子力学里的波函数和电磁场矢量场的规范变换为：
在上述的变换下，电磁场的拉氏量具有不变性。这个规范变换所对应的群，在数学里被称为 群，也就是一维的幺正群（酉群）。
的几何直观可以表示为两维的旋转：
也就是说，对应于上面旋转的“规范变换”，电磁场的拉氏量具有不变性。我们知道，根据诺特定理，对于拉氏量的一台对称性对应于一台守恒量，1941年泡利证明了电磁场的 的对称性，对应于电荷守恒。（这里有些细节，比如“整体对称性”和“局部对称性”，就再展开了。）
杨振宁熟读了泡利1941年的长篇论文。按照杨振宁的回忆：
我在昆明和芝加哥做研究生时，认真学习了泡利关于场论的综述文章。我对电荷守恒与理论在相位变化下不变的关系印象非常深刻。后来我发现这些思想来源于外尔。印象更深的是，规范不变性决定了整个电磁相互作用。 1954年，杨正宁把规范不变性推广到了质子和中子的同位旋理论。
什么叫做质子和中子的同位旋？当中子被发现以后，人们感觉到中子和质子长得真得很像。有没有可能中子是质子的一种“马甲”？海森堡认为，中子和质子本质上是相同粒子处在不同的电荷状态，而这种状态即被称为“同位旋”。
杨振宁试图给出质子和中子强相互作用的一台规范理论，其对应的规范变换下的不变性，恰好对应于同位旋守恒。为此，杨振宁开发出了一套和电磁场的规范变换完全不同的规范。
由于电磁场里有矢量场 。杨振宁为质子和中子的作用开发出一台新的场，称之为B场。和电磁场里的张量形式
而B场的张量形式为：
其对应的波函数和B矢量场的规范变换为：
杨振宁证明，在上面的规范变换下的不变性，恰好对应于强相互作用中的“同位旋守恒”。
杨振宁发明的B场，是第一次用规范场论来刻画质子和中子之间强相互作用的尝试。按照群论的话说，B场具有SU(2)（一阶特殊酉群）的对称性，也就是上面的S满足
我们知道，3维球面上的旋转，可以用三个欧拉角（  ）来表示：
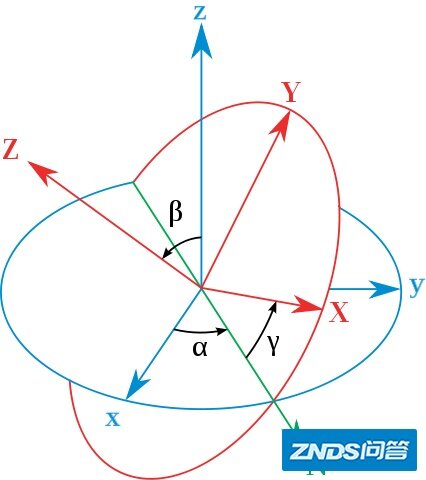
而直观地说，SU(2)对应于四维球面上的一台旋转。
相比电磁场的规范变换群是可交换的，B场的规范变换群是不可交换群（即为非阿贝尔群）。
1954年，杨振宁和米尔斯的论文《同位旋守恒和同位旋场的不变性》
可惜的是，杨振宁的B场拉氏量里没有质量项。我们知道，电磁场对应的粒子是没有质量的光子，所以电磁力是一种长程的里。而倘若B场对应的粒子（学名叫做规范场的“规范玻色子”）不带质量，那么B场对应的也必然是一种长程力，这和强作用力是短程里不相符合。用B场来构建质子和中子之间的强弱相互作用，是不正确的。
由此，杨振宁—米尔斯场因为不含质量在当时就遭到了泡利的抨击。之后，杨—米尔斯的理论被物理学界冷落了10多年。
事实上，杨振宁的思想大大地超越了时代。到了1960年代，在量子场论再次陷入低潮的时候，试图用量子电动力学的方法建立强、弱相互作用理论而失败的物理学家们，再一次把目光盯上了杨—米尔斯场。
新的思想注入老的杨—米尔斯理论，终于使得这个理论成为了标准模型的基石。
4.5 希格斯机制和标准模型
杨振宁—米尔斯的理论深受泡利的启发，但是该理论一出来就遭到了泡利的质疑，其实也是有道理的。在当时，杨—米尔斯场面临了至少三大问题：
- 如何给场对应的粒子加上质量？
- 如何把场二次量子化从而进入到量子场论的范畴？
- 如何对付量子场论里无穷大的问题？（场的重整化是否可行？）
最终这三个问题都被解决了，由此杨振宁的B场正式升级成为“规范场”，而规范场论正式成为了粒子物理标准模型的理论基石。
关于第一台问题，物理学家们最终是用“自发对称性破缺”和“希格斯机制”来解决的。
1960年，旅美日本物理学奖南部阳一郎受到了凝聚态物理的启发，把“自发对称性破缺”的概念引入粒子物理。1964年，英国物理学家希格斯等人同时提出了让规范场粒子产生质量的机制，如今被称为“希格斯机制”。
自发对称性破缺，通常可以用下面的墨西哥草帽图来打比方。
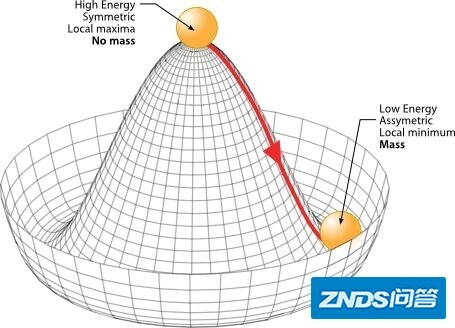
如果一台粒子处在墨西哥草帽的顶点上，看整个系统是旋转对称的。但是在一台微扰之下，粒子跌落到帽子的最低处，在那里的一台局部再看整个系统，就不再是旋转对称的。在这里，微扰下的跌落，可以看成“自发对称性破缺”。当粒子在草帽高点，处在对称之中，根据规范场论，粒子是没有质量的。但是当粒子跌落到草帽低点，则是有可能获得质量的。
至于粒子获得质量的机制，即是希格斯机制。希格斯机制解释起来就比较复杂了，需要规范场和希格斯场相互作用，希格斯粒子和规范场粒子之间还需要通过一种由对称性破缺产生的无质量的标量粒子来作为“中介”，从而使得规范粒子获得质量，这就不再深入展开了。
我们来看第二点，如何把杨—米尔斯场量子化。这个工作倒并不是很难，在1960年代同时有很多物理学家在做。
难点在第三点，如何把量子化后的杨—米尔斯场重整化，即消去计算中冒出来的各种无穷大。还记得吗，在量子电动力学的计算中，也是各种无穷大如同泡泡一样冒出，最后物理学家用了一种耍赖的方法去掉了无穷大，被称为重整化。但是量子电动力学的方法并不能直接被用到杨—米尔斯的场中。一直到了1971年，荷兰物理学家霍夫特（当时或是博士在读学生）和他的老板提出了一套“维度正则化”的方法，重整了自发对称破缺下获得质量的杨—米尔斯场。
杨—米尔斯场的重整化
自此，杨—米尔斯理论的困难被基本扫除，杨—米尔斯理论升级成为规范场论，而规范场论迅速成为了统一粒子理论的基石。
下面我们就来简单地看看粒子物理的标准模型。
标准模型里有61种基本粒子，其中包括了36种夸克，12种轻子，8种胶子，2种W粒子和一种Z粒子，另外还有光子和希格斯粒子。
夸克有2个种类，3个世代，一共六味：上、下、粲、奇、顶、底。另外每个味的夸克还有3种色（色荷），所以一共有18种夸克。加上对应的反夸克，所以夸克一共有36种。
轻子，主要是电子，渺（  ）子，陶（  ）子，其对应的中微子，及其反粒子。
夸克和轻子具有半奇数的自旋，被称为费米子。费米子组成了世界上的物质。
其它的粒子具有整数的自旋，被称为玻色子。玻色子负责传递各种作用力。
其中大家熟悉的，就是传递电磁作用（力）的光子。光子无质量，所以电磁力是长程力。1950年代物理学家们建立了电磁作用的量子场论，即是量子电动力学。
负责传递弱相互作用力的被称为中间玻色子，即W及Z玻色子。比如下图给出了 衰变的费曼图，可以看到重W玻色子衰变成的电子和反电微中子，整个过程由  玻色子传递。
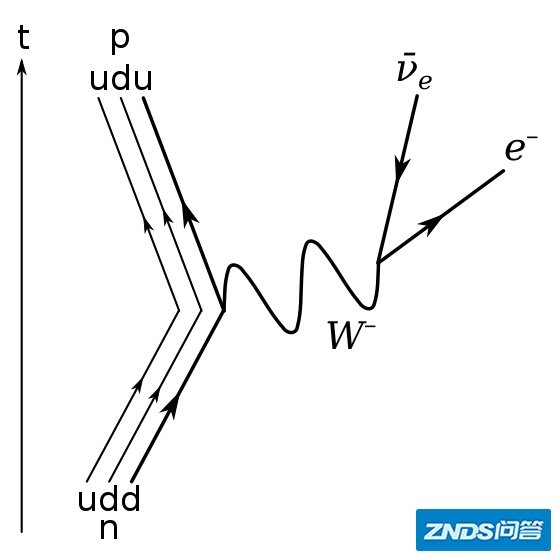
两种W及Z玻色子，可以用杨—米尔斯场的对称性来刻画，而它们的质量通过希格斯机制来获得。理论粒子物理学家凭空预测了弱相互作用的三种中间玻色子，1983年被欧洲粒子加速器的实验找到。
格拉肖，萨拉姆，温伯格因为提出电弱统一理论而获得1979年诺贝尔物理学奖
负责传递强相互作用的，当初汤川秀树认为是“介子”，其实不然。传递强相互作用，是指夸克之间的相互作用，是通过交换“胶子”来实现的。胶子的规范场，满足SU(3)对称性，比中间玻色子的SU(2)多出一阶。另外胶子是没有质量的，所以不需要希格斯机制帮忙。没有质量的规范粒子，难道不应该是一种长程力？为了解决这个问题，一种叫做“夸克渐近自由”的补丁被打到了夸克理论里。也就是说，夸克和胶子之间的力，是越近越小。
只有光子和胶子不和希格斯子作用。希格斯子非常厉害，它通过希格斯机制给予W及Z玻色子，又通过汤川耦合给予各种费米子（部分）质量。希格斯子曾近被不少人认为是了让规范场论可以处理中间玻色子而人为拼凑出来的理论（比如，格拉肖称希格斯子是温伯格的“厕所”），但是在2013年，希格斯子居然被发现了，至此标准模型里预测的粒子全部被发现。
统一标准模型的理论，是规范场论，也就是从杨—米尔斯场升级而来的规范场论。
首先，物理学家们把电磁作用和弱相互作用统一起来，电磁（光子）的规范场具有U(1)对称性，W及Z的规范场具有SU(2)对称性，而两者合起来的规范场的对称性为SU(2) x U(1)。这个“合起来的规范场”不是简单地把两个规范场乘起来，而是说具有SU(2) x U(1)对称性的规范场通过自发对称破缺后，通过希格斯机制，同时生成了W，Z玻色子和光子。在~ 200GeV的能级以上，电磁力和弱作用力统一成“电弱相互作用”，而不再有单独的电磁力和弱力了。
至于强相互作用，在标准模型中独成一派。胶子对应的规范场具有SU(3)的对称性。描述夸克、胶子之间强相互作用的学问，叫做量子色动力学（QCD）。
电弱统一理论和QCD合二为一，即是标准模型。
到目前为止，标准模型是物理学家们达成共识的一台模型。当然，理论家们当然不会止步在标准模型的。在它的基础上，各种各样的新模型又被建立起来了。
五、超越标准模型
5.1 标准模型的缺陷，大统一理论
标准模型是目前实验可以验证的理论最前沿。
但是，根据物理学家们的“信仰”，标准模型远远不是最终到达的宇宙终极解释 ToE。
首先，标准模型只涉及强、弱、电磁作用力，而没有把引力囊括进来，不符合物理学家对于终极理论To的信仰。
其次，我们知道宇宙中有标准模型没有包括的粒子，比如暗物质粒子。宇宙学的精密测量告诉我们，暗物质粒子并不是标准模型里的普通粒子。
第三，标准模型里的正反粒子是对称的，为啥现实宇宙中基本上都是正粒子？反粒子都去哪里了？
单单从“美学”的角度出发，标准模型也是不完善的。该模型里有至少19个自由参数，这或是在没有考虑到中微子质量的情况下。打上中微子有质量的补丁，又要增加7到9个参数。这些参数都要靠实验来决定。要知道牛顿的万有引力只有一台参数，而真空中的麦克斯韦方程也只有一台参数。我们的世界，真得需要标准模型里提到的这么多参数来决定吗？
另外一台问题，即是希格斯粒子的等级问题（Hierarchy problem）。
简单地说，如果希格斯粒子是其它各种基本粒子获取质量的根源，那么物理学家认为希格斯粒子应该和一种称为“普朗克质量”：
处在一台量级上。为啥在事实上，希格斯粒子的质量和普朗克质量相差如此多的级别？
为了解决这些问题，一台自然而然的突破口，就是能否把强相互作用力和电弱作用统一起来？
这里要强调一点，标准模型里只在规范场论的框架下包括电弱统一理论，却并强、弱、电磁三者统一的理论。
于是当初提出电弱统一理论的三人之一的格拉肖和他的合作者提出了SU(5)理论。我们知道，强作用的规范场具有SU(3）对称性，电、弱作用的规范场分别是SU(2)和U(1)对称。一台更高级别的对称，就是SU(5)（5-阶特殊酉矩阵）：
三种力在大约10^15 - 10^16 GeV的能级下，统一在SU(5)的规范场中，随着能量降低而产生对称性破缺，强力从中独立出来，而后在~200 GeV的能级下，电弱两种力也分了开来。
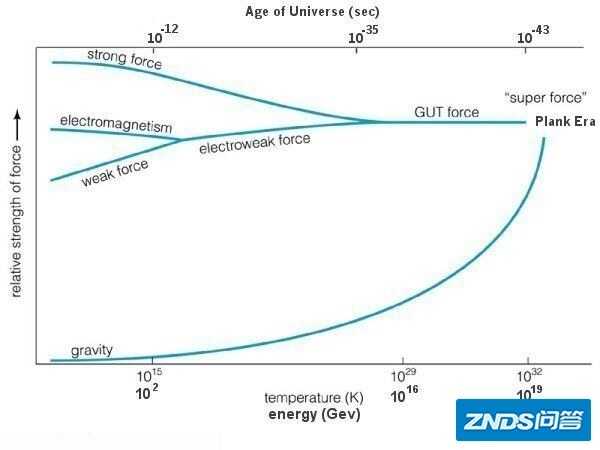
弱相互作用力和电磁作用力在大约246 GeV的能级统一成为电弱作用。大统一理论认为在10^15 - 10^16 GeV 左右电弱作用将和强作用统一起来，成为“统一的力”。而“统一的力”可能在更高的能级上和引力统一起来。
格拉肖和合作者的思路，目前被称为Grand Unified Theory（GUT），叫做大统一理论。这个理论最大的问题是：重子数在规范场中将不再是守恒量。也就是说，质子也是会衰变的，理论预测了质子衰变的时标是10^30 - 10^31年。
可是，这个预言已经被日本的超级神冈探测器否决了。
值得一提的是，超级神冈探测器原本是为了测量质子的衰变，然而并没有观测到。但是，失之东隅，收之桑榆。超神冈最终探测到了中微子振荡，解决了“太阳中微子失踪之谜”，当然，这是另外一台话题了。
超神冈切伦科夫探测器
于是人们开始考虑更大的对称群，比如SO(10)对称的规范场，虽然SO(10)的理论依旧预测质子衰变，但是给出了各长的估计，可以让实验暂时无法验证或否定这些大统一理论的模型。
迄今为止，没有任何证据显示质子可以衰变，而质子衰变的下限已经被超神冈限制到了10^34 - 10^35 年。以下是各种大统一理论对应的质子衰变时标和对应的实验情况，前面几个模型已经被否定，而很多模型实际上也被几乎否定：
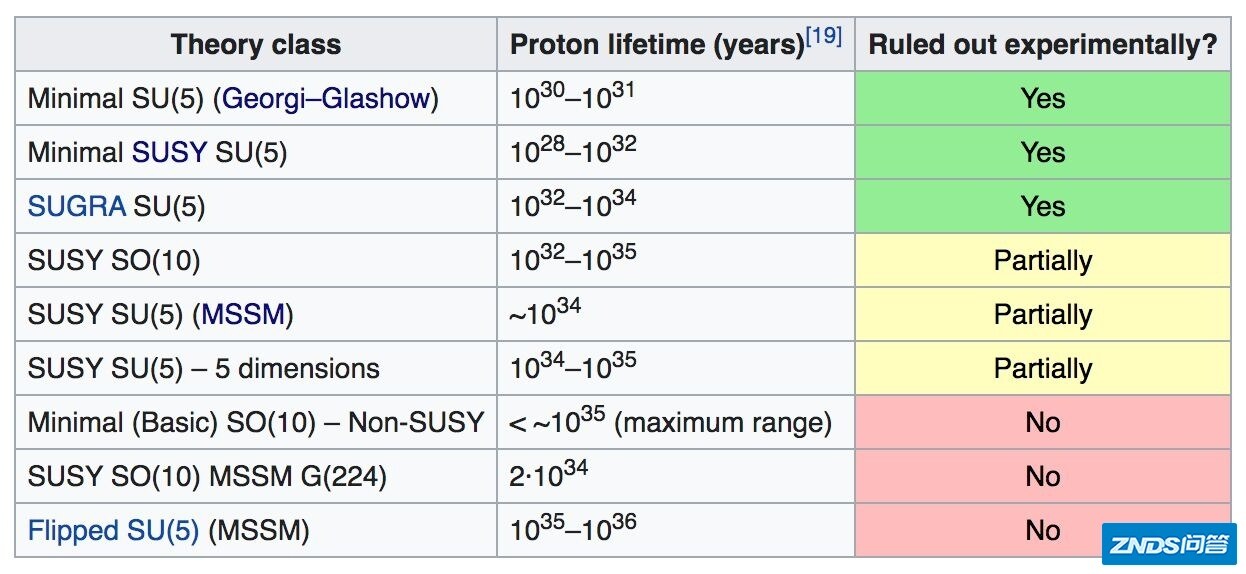
上面的表格中，SUSY指的是超对称（supersymmetry）。比起GUT，另外一台更宏大的模型假说就是——超对称。
5.2 超对称
海森堡当年认为质子和中子是一种粒子，从而引入了“同位旋”的概念。杨振宁和米尔斯在同位旋的概念上引入了规范场的对称性，由此成为了粒子物理统一理论的基石。
对于“超对称”来说，最直观的物理思维，是把费米子和玻色子看成同一类粒子。这种对称性要比“同位旋”要复杂很多，但是其基本思路却是差不多的，就是让看起来不同的粒子成为同一类。
超对称的概念最早是由日本物理学家宫泽弘成在1966年提出的。到了70年代，世界上很多物理小组几乎同时发展了超对称的模型。从那时候到目前，至少已经出炉了数万篇讨论各种超对称模型的论文了。
我们知道，费米子具有半奇数的自旋，满足泡利不相容原理（从量子统计的角度来说，叫做“反对易性”），但是具有整数自旋的玻色子，并不满足泡利不相容原理（“对易性”）。标准模型中这两类粒子是独立的，但是超对称认为它们来自于同一台本原，两者可以相互转换。
从数学上来说，如果说狭义相对论里的洛伦茨变换是建立在四维时空上的“坐标旋转”，那么超对称的群，可以表达成远高于四维的超空间里的一台类似洛伦茨变换的“坐标旋转”（准确地说，是庞加莱变换，参考讨论“狭义相对论和不变量”的那一节），外加上费米子和玻色子相互转换的内禀对称性。
超对称做出了一系列奇妙的预言。其中最大的预言，就是预言了大量的超越“标准模型”的新粒子。如果将标准模型原有的粒子增加一倍的超对称，也就是“最小超对称模型”（MSSM），如下图所示：
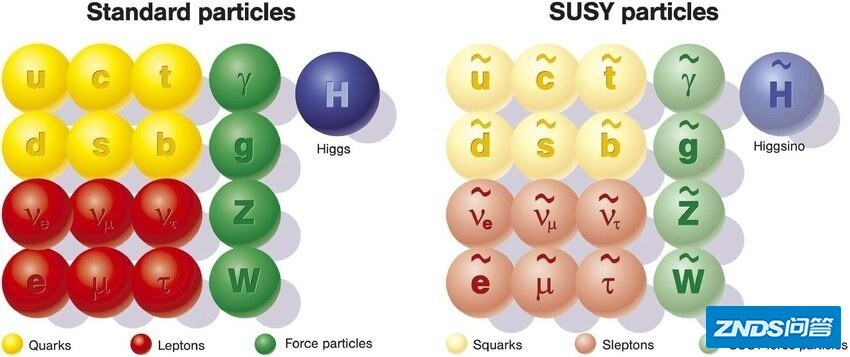
上图中，左边对应着标准模型里的各种基本粒子，而每一种粒子在右图都对应着一种“超伙伴粒子”。也就是说，在左图里的费米子，在右图有一种玻色子作为它的“超伙伴”，而玻色子则对应着一种费米子为“超伙伴”。
比如，电子的自旋为1/2，应该有一台自旋为零的胖伙伴，叫做超电子。中微子和夸克的伙伴分别是自旋为零的超中微子和超夸克。这些都是费米子对应的玻色子伙伴。光子的对应伙伴为自旋为1/2的光微子，而W，Z也分别对应自旋为1/2的W微子和Z微子。
基本粒子和作为“超伙伴”的超对称粒子在数学上是可以通过超对称变换而相互转换的。
根据超对称理论，超对称粒子要比标准模型中的基本粒子质量大很多。比起标准模型19+7的参数自由度，超对称的模型更是增加了参数（调参）的个数。单是最小超对称模型MSSM，就具有105个参数，物理学家们可以通过“调参”来调节超对称粒子的质量。即便如此，物理学家从“美学”的角度出发，或是希望能够把超对称粒子的质量“调”得小一点。
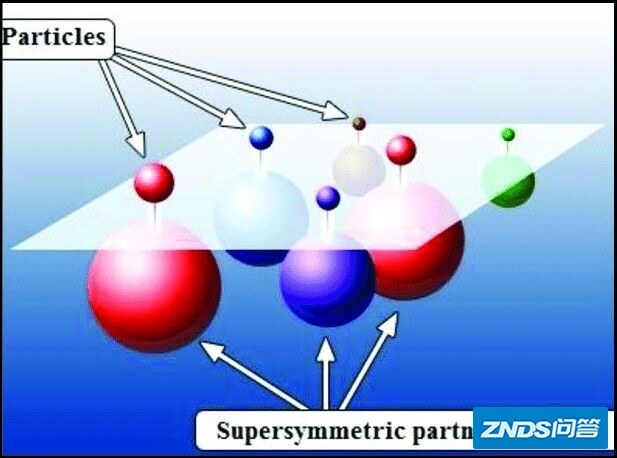
来源：https://www.researchgate.net/figure/Particles-and-supersymmetric-partners-provided-by-the-supersymmetry_fig3_277651546
具体说来，如果超对超粒子可以和普通粒子发生作用，粒子质量应该粒子与这个宇宙相互作用的大约是在弱作用范围到顶夸克的质量之间，也就是大约100GeV左右的质量。
很无奈的是，目前欧洲LHC（大型强子对撞机，后面我还会说到这个大装置）并没有在100GeV乃至于1000GeV（1TeV）的能级发现任何超对称粒子。夸克的超对称粒子超夸克（squark）的质量已经限制到1.1TeV 以上。而胶子所对应的胶微子（gluino）也被LHC排除了1 TeV以下的可能性。
欧洲LHC（大型强子对撞机）的大小：周长27公里。
另外，关于暗物质粒子的实验也表明，目前并没有发现任何100GeV左右质量的新粒子和普通物质进行作用的迹象。
以下的示意图给出了各种超对称粒子的质量限制，注意蓝色的代表LHC给出的下限，红色的暗物质粒子测量给出的上限：
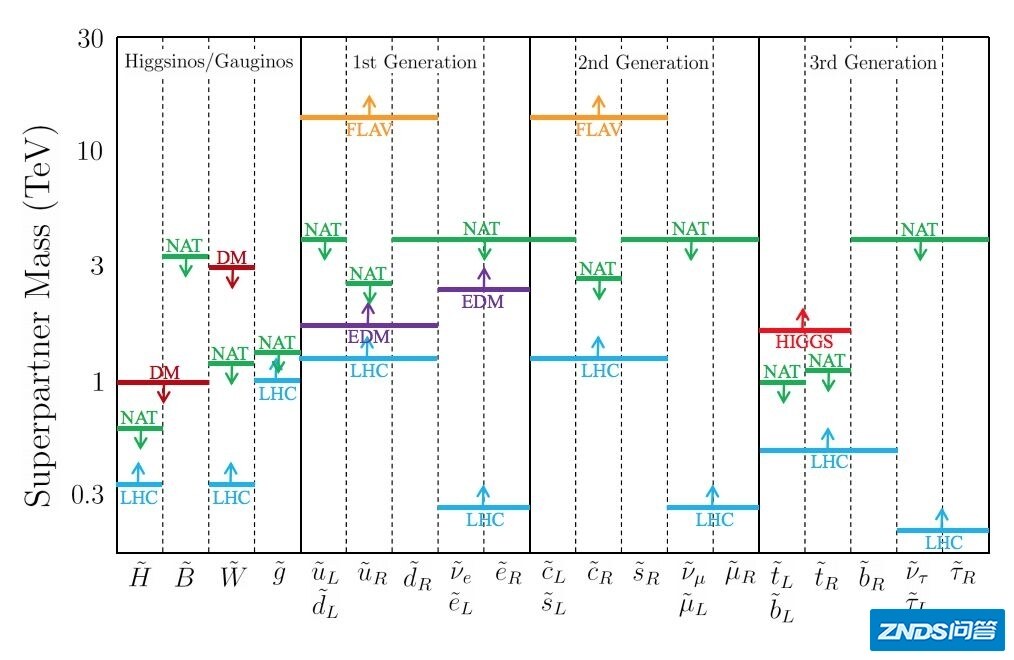
超对称粒子的质量限制，来自Feng(2013) https://arxiv.org/abs/1302.6587
虽然超对称的理论家们顽强地把预言的超对称粒子质量继续“调”得重一点，把模型搞得更复杂一点，但是不少人已经开始放弃这个曾经大流形了40年的超对称理论了，他们更愿意直接拜倒在标准模型之下，不再前进了。
下面我们就来看一下弦论的历史。
5.3 初代弦论
弦理论最早是为了解释强相互作用而提出来的。
在描述夸克和胶子作用的量子色动力学（QCD）被完善以前，物理学家并不百分百地相信夸克模型，其它理论也尝试着诠释强相互作用。弦理论也在这时候应运而生。
1969年，旅美日本物理学家南部阳一郎在一次物理会议上，别出心裁地提出，只要假设强子是一种犹如谐振子模式振动的弦，而非点粒子，那么就可以解释一种被称为“Regge关系”的强子激发态的实验结果。
我们知道，基本粒子是不考虑粒子的大小的。基本粒子把一台几何学上的“质点”赋予了一系列的性质，比如质量、电荷、自旋等，却没有任何空间上的尺度。19世纪末，当时电子被发现没过多久，物理学家们曾经把电子当成一台球体，却发现根据经典电磁学得到的电子尺度实在太大，而后粒子就被当成一种“质点”的存在。然而，截止60年代末关于强子丰富的实验结果，让南部猜想强子可能具有一维的振动模式。不久之后，尼尔森、萨斯坎德（Susskind）也提出了和南部很类似的弦模型。
南部阳一郎，来自日本的天才物理学家。初代弦论的提出者，也是自发对称破缺的提出者，从而复兴了杨米尔斯的理论。
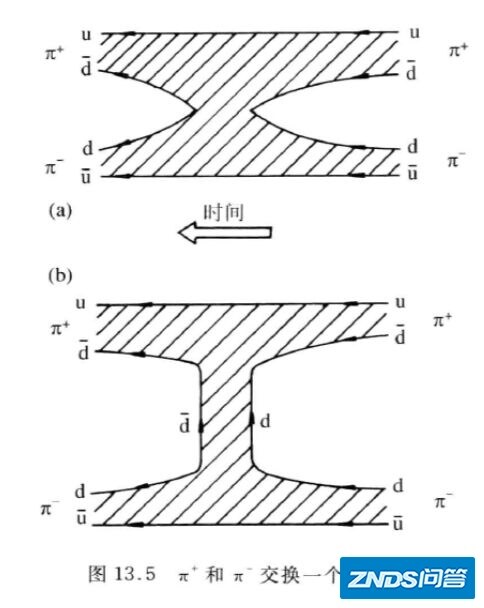
南部阳一郎首先提出强子的“弦模型”，即重子（三个夸克之间）或者介子（两个夸克之间）的振动弦模型。这是南部在他的科普书《夸克》里的介子弦模型下的费曼图。
可是，强相互作用的“弦论”并不成功，该理论出现了一系列的和实验不相符合的计算预测。与此同时，量子色动力学正在一统江湖，成为了描述强相互作用的最终理论。强相互作用的“弦论”由此寿终正寝。
即便如此，强子的弦模型，或是在某些人的心中播下了“美学”的种子。当量子色动力学崛起和标准模型一统江湖的时候，有人长期游走于当时的主流粒子物理学之外，开启了执着的“弦论”之旅。其代表人物，就是施瓦茨（John Schwarz）。
1974年，施瓦茨等弦论家们绕开了粒子物理学的主流，把弦论应用到了“量子引力”上。
直到目前，我的这篇科普长文一直在说粒子物理，几乎没有提到过引力。
迄今为止，引力理论的最终版本，依然是爱因斯坦的广义相对论。
事实上，如果物理学的终极目标是要找到一台统一的ToE理论，那么一定就要统一“量子力学”和“广义相对论”，让它们融合在一台框架之下，用来证明我们的宇宙来自于一台统一的起源。
比如，下图是物理学从经典物理到理想中的“量子引力学”的走向：
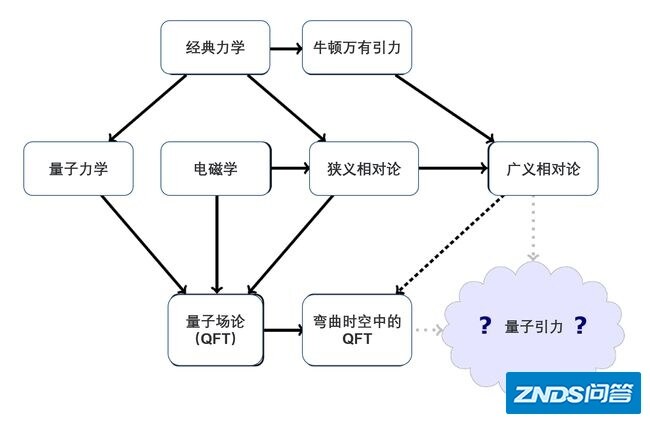
或者看看下面这张ToE的“走向图”：
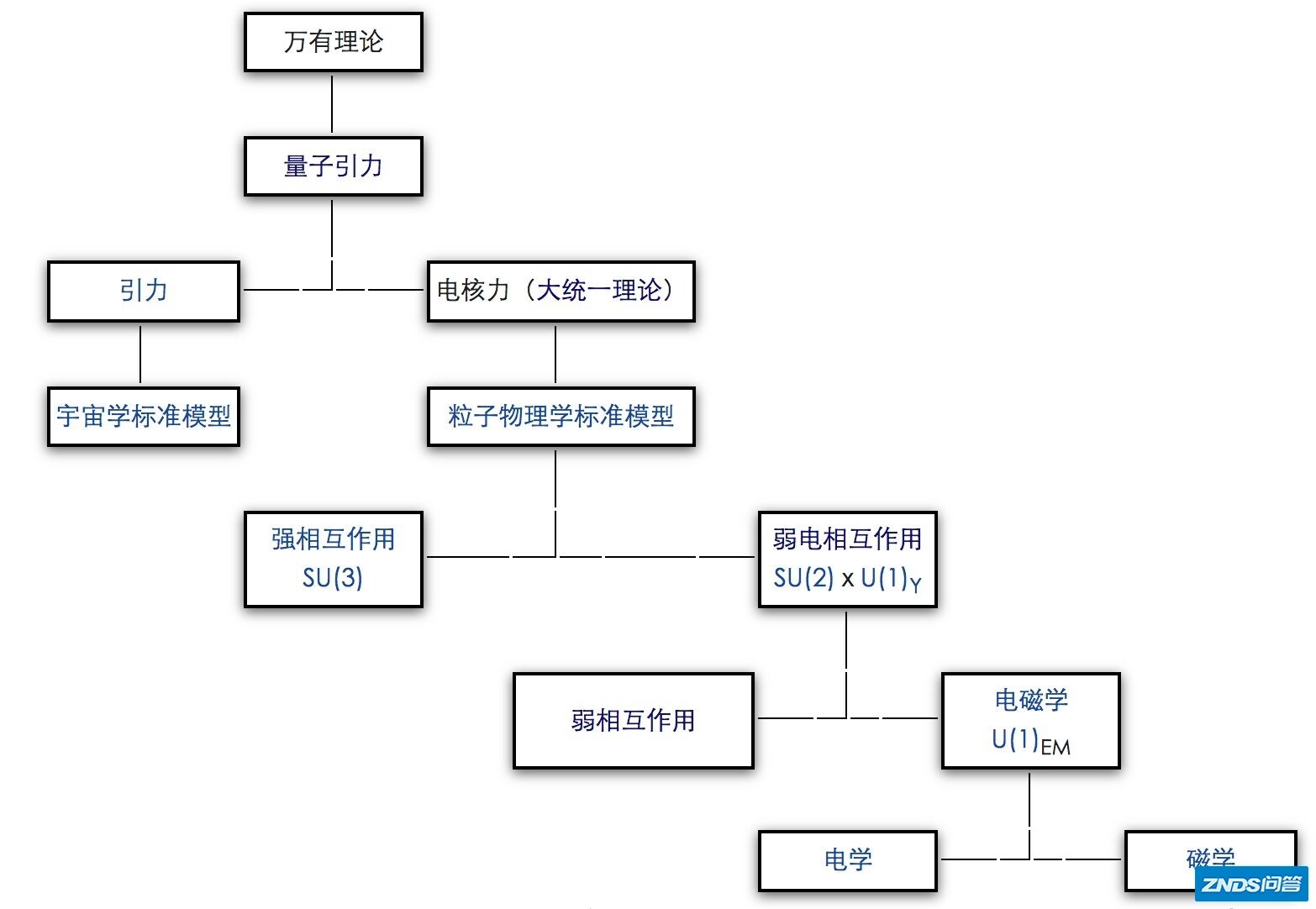
统一量子力学和相对路的目标实在太大，我的这篇科普承载不了这个大话题，只能简单地从粒子物理的角度来说一下引力：
经典物理被量子力学被实行了量子化，再通过量子场论、规范场论的引领，量子力学被实行了二次量子化，建立起粒子物理的标准模型。一台自然而然的想法就是，能否对广义相对论进行量子化？
前面提到，在标准模型里，强力、弱力和电磁力都是通过玻色子传递的。那么倘若要把引力量子化，那么在量子化的“引力场论”里，引力自然也是由中间玻色子传递的。早在1930年代，泡利和他的合作者就发现，自旋为2的无质量的“引力子”是量子化广义相对论的必然。
但是引力场量子化遇到了巨大的困难。人们即不能通过量子电动力学的重整化方法来“驯服”场的发散计算，也不能通过规范场论的方法来去除发散。理查德•费曼曾经对引力的量子化做了很多工作，但是最后他失望地说，他不想参加关于引力的任何会议了。
就在量子引力遇到重重困难的时候，施瓦茨等人把弦论和量子引力联系了起来。他们研究了玻色子的弦论，发现了弦的模型里会自动出现一种自旋为2的无质量粒子，神似引力子。由此，“玻色子弦论”着实被研究了一阵子。
发现玻色弦论可以包括引力子的三位物理学家，可是他们的研究在当时是非主流（http://zhishifenzi.com/depth/character/11085.html）
除了引力子外，玻色子弦论里还出现了一些奇怪的粒子，比如快子（超光速的粒子）和胀子。由于假象的粒子并没有实验上的任何支持，更由于超对称的思想使得人们把费米子也加入弦论之中，所以独立的波色子弦论很快也寿终正寝了。
不过，玻色子弦论在落幕之前或是拓宽了人们的思路。当时的人们把弦模型分成两种：开放的弦和封闭的弦。为了消除封闭的弦模型里的快子问题，有个叫爱蕾丝（Lovelace）的物理学家把弦的时空放到了26维，也就是25维的空间，加上一维的时间。
虽然推导26维的过程很复杂，但是这里可以做一台简单的化简，让大家体验一下。设维度为D，那么协变性要求经过一系列的复杂计算，最后要求：
一般情况下，我们知道  也就是1+2+3+4+......是个发散的量，是无穷大，所以上面的等式必然不成立。
然而，量子场论的重整化“耍赖皮”，可以化无穷大为有限，重整化理论告诉我们（术语叫做“黎曼zeta函数重整化/正则化”）：
由此，前面的维度方程可以推出(D-2)/24=1，也就是D=26。
至于为啥无穷级数可以得到奇怪的答案，这是20世纪初印度数学家玛拉努金的脑洞，可以参考以下的资深问答：
“在那之前，做粒子物理的从未有人考虑过四维以上的时空。”施瓦茨回忆说。
1972年，施瓦茨升级了玻色子弦论——把超对称引入弦论，从而把玻色子弦论的26维降到了10维。
其实，超对称框架下的弦论要求10维，是不难理解的。数学上也是简单的。以下原封不动地把关于“超弦教科书”上要求弦论10维的推导贴上来：
来自David Tong的弦论讲义（http://www.damtp.cam.ac.uk/user/tong/string.html）
由此，基于超对称，玻色子弦论的26维，变成了超对称弦论里的  。
和很多科普书上介绍的不同，弦论所要求的10维，并不是“第一次超弦革命”的产物，而是早在弦论的史前时代（1972年）就被推导出来了。但是，这并没有太多用处，弦论在未来的10多年里并没有太多进展。
六、弦论
6.1 粒子物理实验时代的“分水岭”
让我们来看看1984年所谓“第一次超弦革命”之前的粒子物理。
那一年，量子物理学界的元老保罗·狄拉克去世了。他在生前一直反对量子场论，认为量子场论的重整化里涉及到无穷大减去无穷大，就是一台数学上的笑话。换句话说，他老人家绝对不信什么1+2+3+4+... 最后会等于-1/12，简直就是鬼扯。
但是绝大多数物理学家早已经接受了量子场论及其重整化的技术，量子场论也成功地被升级成为规范场论，成为了标准模型的理论基础。量子电动力学、电弱统一理论和量子色动力学都已经基本完善，大部分夸克都已经被实验验证，前一年（1983年）W和Z中间玻色子也被实验验证，并在这一年（1984）迅速拿到了诺贝尔物理学奖。除了顶夸克要等到1995年，希格斯粒子要到2012年才被发现之外，标准模型已经很“完善”了
大统一理论还有待验证，其中一台关键是质子衰变，但是1984年的时候质子是否衰变还没有结论。超对称也被提出10多年了，一大批新的“影子粒子”被预测出来，但是实验依旧遥遥无期。
曾经，只有极少数的人依旧在关注弦论。然而到了1984年，一切都变了。
来见识一下实验粒子物理从40年代末到80年代初发现新粒子的速度：
新粒子发现时间表
大量粒子被发现，大量的理论被推出来解释新粒子，最终标准模型脱颖而出，这完全是由实验促进的。
然而，这一切恰好在1984年终止了。
1984年以后，除了前面提到的顶夸克（1995）和希格斯粒子（2013），粒子实验唯一“拿得出手”的新进展，就是关于中微子振荡和中微子质量的实验观测了。
粒子物理的“实验时代”，可以说是以1984年中间玻色子的诺奖为分水岭，就此黯淡下去了。而这一年，被称为超弦理论的“第一次革命”的年份，和粒子物理实验时代的分水岭是同一年，这是不无巧合的。
这一年，坚持留守在弦论阵地上的施瓦茨，和他的合作者格林推出了超弦的“反常消除”模型。大量由于没有新实验结果从而“处在失业边缘”的理论物理学家们（由于消息的滞后性，他们的队伍依旧在持续扩张），成百上千地涌入超弦理论。
6.2 格林—施瓦茨定理
什么叫做规范反常？反常（anomaly）指的是某些经典的对称性（守恒律）在量子理论中被破坏，那么这种破坏就被称为反常。规范反常，是指量子场论的处理破损坏规范对称性。
规范反常必须要被抵消，否则理论本身是不自洽的。标准模型里，一代费米子对规范反常的贡献相互抵消，由此可以断言标准模型是自洽的。
糟糕的是，10维的弦论模型存在着规范反常，这表明弦论是不自洽的。这一直是困扰弦理论的一台“拦路虎”。
直到1984年，施瓦茨和合作者格林证明了，在特殊的规范群SO(32)或者E8  E8下，弦论的规范反常是可以消去的。这被称为格林—施瓦茨定理。
SO(32)，说的是32阶的特殊正交群。
E8的定义和李群研究多维对称结构有关。具体来说，E8是一种具有248维度的对称结构。以下是这种对称结构在2维的家用投影:
E8 X E8是两个E8群的外直积。
来一台段子：
根据施瓦茨的回忆，他在一台暴雨雷电交加的晚上，证明了弦模型在这两个特定的规范群下反常可以被消除，方程里的数百项“神奇”地消去了。那天晚上的天气是如此之坏，是因为上帝不想把他的秘密展示给人类。
6.3 卡拉比—丘空间登场
格林—施瓦茨定理表明，弦论可以消除反常，称为一种自洽的理论。
弦论还具有另外至少三个优点。
第一，弦论不需要量子场论所需要的（耍赖皮的）重整化技术。重整化的目的是在量子场论中消去无穷大的量。如果刨根究底为啥量子场论会出现无穷大，那是因为其假设了各种粒子是没有大小的“点粒子”。弦论就没有这个问题。弦论假设的弦在普朗克尺度上振动，将不再有费曼图里粒子相会的“顶点”，费曼图将变得“光滑”：
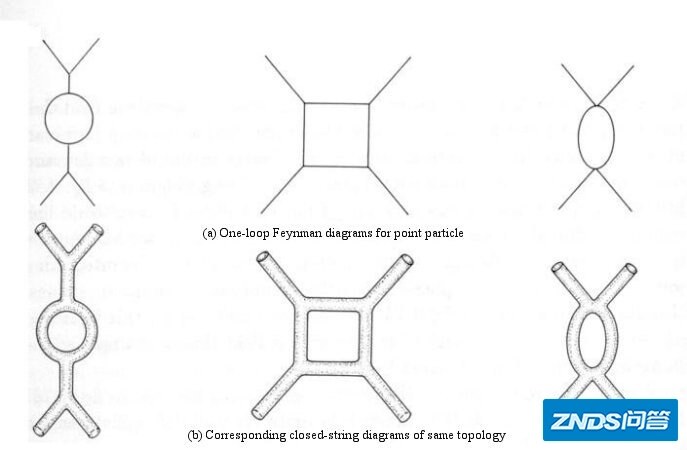
第二，弦论自动包括了引力子，可以看成囊括了量子引力的精华。
第三、弦论把粒子看成振动的弦，所以粒子的质量来源于弦的振动模式，而非希格斯机制。
当然，上述第一点和第二点早就被施瓦茨之类的弦论家知晓，而格林—施瓦茨定理则是打通了“任督二脉”，从而弦论一跃成为缺乏实验结果的时代里理论物理学家的宠物。
接下来的问题是，如果弦论要求世界是10维的存在，那么为啥我们的时空只有四维，而别的六维又是如何样的存在？
1985年，四个普林斯顿的物理学家格罗斯（David Gross），和Emil Martinec、Jeffrey Harvey、Ryan Rohm（号称“普林斯顿弦乐四重奏”）基于SO(32)和E8 X E8的对称性，发展出一套混合弦的理论，可以完美地融合玻色弦的26维振动和超弦的10位振动，由此被称为混合弦理论，也叫杂化弦理论（Heterotic string theory）。
同一年，开头提到的斯特鲁明格、威腾，还有第一、第二作者坎德拉斯、霍洛维茨在丘成桐的帮助下证明了：卡拉比—丘成桐定理所描述的空间，恰好满足了弦论里多出来的六维所要求的结构，也就是必须是里奇平坦（真空的结构），并且满足一定的超对称性（具体地说，要满足SU（3）的和乐（holonomy）对称性，这里的微分几何术语以后再介绍）。
另外很关键的一点是，弦论多出来的六维空间和我们四维时空最大的不同是，这六维空间是“紧致”的，通俗点说，就是“有大小的”，而不像通常的四维时空那样可以无限延伸的。而卡拉比—丘成桐空间的紧致性，也恰好满足了物理学家的要求。
于是弦论家和数学家（丘成桐）一拍即合，卡拉比—丘成桐流形成为了弦论的一大数学（几何学）基础。
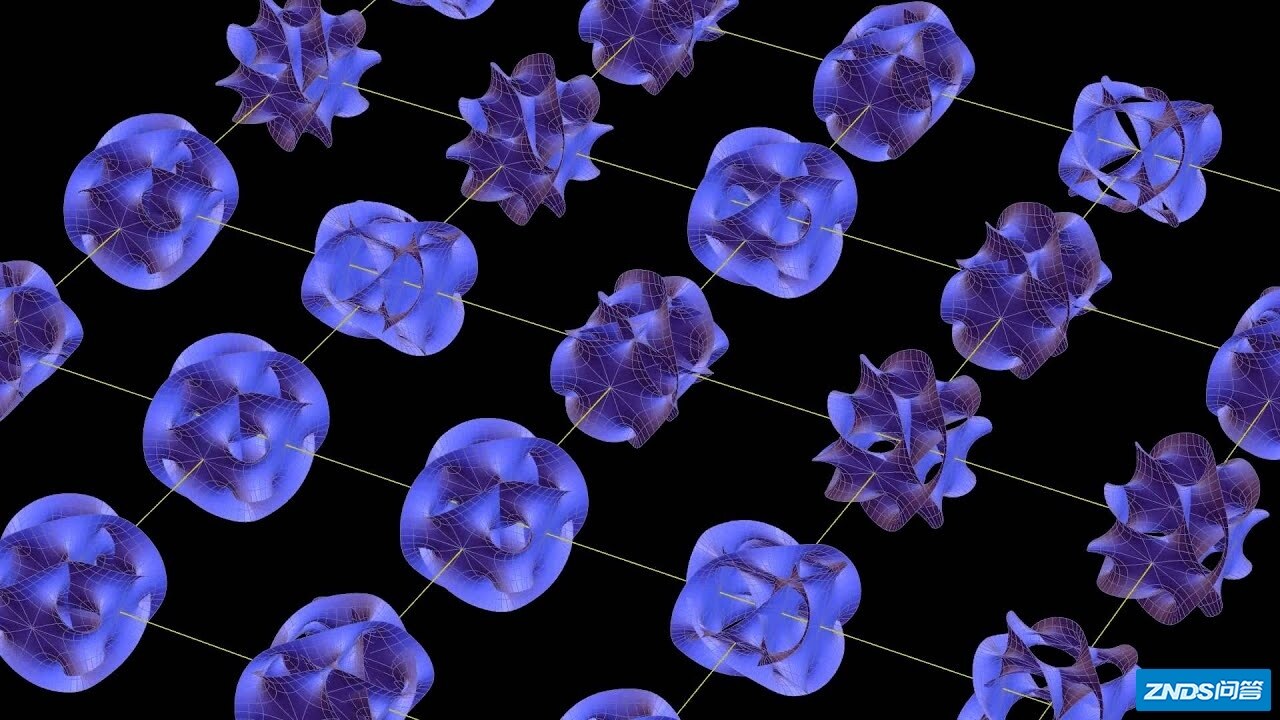
由于弦论要求的卡拉比—丘流形（空间）是六维的（复数三维），很难用直观表示，所以一般人们画出卡拉比—丘流形的三维“家用投影”：
又由于“四维时空”和“六维卡拉比—丘流形”的乘积形式很难直观，通常人们把四维时空化成延展的两维时空（平面），把许多卡拉比—丘空间的三维家用投影整齐地画在两维平面上，用来展示弦论的10维结构。
可以消除反常的对称性，以卡拉比—丘空间为基础的10维结构的提出，使得弦论一下子成为了粒子物理的最大热门，这就是物理学家们津津乐道的“超弦的第一次革命”。
不过，在这场革命的喜悦下，潜伏着各种危机。
首先，弦理论不是一种，而是五种，到底哪种才是“真正”的弦论？
其次，就像丘成桐说的那样，卡拉比—丘空间不是唯一的，而是具有庞大的数量。我们如何样来进一步限制卡拉比—丘空间的性质，从而减少弦理论所需的10维时空的自由度？
第三点，弦论是建立在超对称的基础上的。但是超对称没有任何实验验证，这该如何破？
七、小结
我们来小结一下这篇长文。
用数学的方法来追求第一性原理，至少从柏拉图的时代就开始了。柏拉图的《蒂迈欧篇》用四种正多面体来模拟四元素（水、土、火、气）的微粒。物理学家追求终极理论（Theory of Everything，简称ToE）的梦想，是和柏拉图一脉相承的。
20世纪初，物理学家试图统一微观和宏观，于是在原子内部建立了“土星模型”（长冈）和“太阳系模型”（卢瑟福）。但是这种单纯从物理图像上建立统一模型并不成功。另外一种思路来自于数学家，即从变换群的角度来看待狭义相对论。1872年，克莱因的《爱尔朗根纲领》从变换群和不变量的角度来统一19世纪的几何学（微分几何除外），这种思路被庞加莱运用到了狭义相对论之中。到了1916年，数学家诺特又把不变性/对称性和物理的守恒律联系了起来，后来对称性的思路被希尔伯特的接班人、数学家外尔引入物理学，逐渐变成物理学中最重要的概念。
场论原本来自于经典力学里对于多体问题的化简和对于引力场的数学思考，后来被法拉第引入电磁学并发展出经典场论。量子场论的出发点是为了研究多粒子的量子理论。对于单个电子的波函数可以用薛定谔方程来描述，但是这是非相对论型的。相对论型的电子方程需要用狄拉克方程来描述。但是狄拉克方程里出现的“负能量”导致狄拉克发展出初代量子场论，也就是“狄拉克电子海”和正电子的理论。量子场论进一步发展出了量子电动力学（QED），也就是研究光和物质作用的量子理论。物理学家用“重整化”的作弊技巧处理量子电动力学中出现的无穷大。
但是QED的理论无法直接运用到强相互作用和弱相互作用里。早在1954年，杨振宁和米尔斯就提出了“杨—米尔斯场”的理论，当初的目的是构建出一种新的场，用来统一质子和中子的“同位旋”。由于杨—米尔斯理论的一系列问题（比如场对应的粒子没有质量），使得该理论被冷落了好多年。之后，“自发对称性破缺”、“希格斯机制”、“非阿贝尔群的可重整化”使得杨—米尔斯理论升级成规范场论，从而成为标准模型的理论基石。
四种力的第一台统一模型，是电弱统一理论，建立在规范场论的基础上。理论先行，随后弱相互作用规范场的中间玻色子也被找到。强作用力的理论建立在夸克模型和规范场的基础上，最终发展出量子色动力学（QCD），也就是夸克和规范场粒子胶子之间作用的理论。标准模型就是由电弱统一理论和QCD合二为一的。
但是有情怀的物理学家们对标准模型并不满意，于是开始寻找更接近ToE的理论。首先的候选理论叫做大统一理论（Grand Unified Theory，简称GUT），即在相当高的能量上（10^16 GeV）可以统一电磁、弱、强三种作用力。大部分的GUT理论都预测了质子的衰变，但是目前的实验很大程度上限制了GUT，也否定了其中不少的模型，比如格拉肖的SU(5)模型。
一种更具有美学效果的理论被提了出来，那就是超对称。超对称的直观思路是把费米子和玻色子（它们的自旋不同）统一起来，有点像当年海森堡用同位旋统一质子和中子一样。超对称最大的预言，就是自然界还存在着大量未被发现的基本粒子，和标准模型里我们已知的普通粒子相互对称，比普通粒子要重（很多）。超对称预言的新粒子至今仍然没有被找到，不靠粒子物理吃饭的物理学家们对于超对称的信仰正在动摇。
弦论很早就出目前粒子物理学里了。早在量子色动力学还没有成熟的时候，强子的弦模型就被提了出来。后来物理学家提出一种叫做“玻色子弦”的理论，最终弦论演变成基于超对称的理论，这就注定了弦论的效应比超对称还要难以发现。从纯理论上的自洽来说，让弦理论家们很激动的时刻，就是弦论可以自动包含引力子、基于超对称的弦可以存在在10维之中、在特定的规范群下弦论可以达成“反常消除”，从而成为自洽的理论。特别是第三点，造就了弦论所谓的“第一次革命”。
借助着弦论第一次革命的东风，人们开始认真理解弦论所要求的10维结构。其中4维是相对论带给我们的四维时空，另外6维是指什么？物理学家认为另外6维非常小，蜷缩附在4维之上。而根据这六维空间的性质，物理学家锁定了卡拉比—丘成桐定理里描述的空间（流形），卡拉比—丘流形成为弦论的数学基础。
（待续）
本系列上篇： |
用Deepseek满血版问问看
